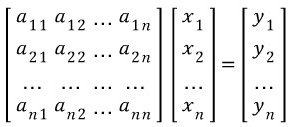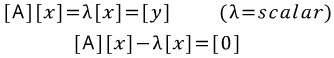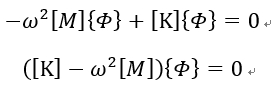야금야금 CAE: 꿀바른 HyperWorks (제 27편 Modal Analysis Using OptiStruct)

한국알테어의 YUNA 입니다!
유한요소해석에 관심있는 모든 분들을 위해 간단한 이론과 HyperMesh를 이용해서 FEA Process를 차근차근 배워보는 “야금야금 CAE: 꿀바른 HyperWorks”를 연재합니다.
1년에 걸쳐 연재할 예정이니 앞으로 야금야금 함께 배워요!

제 27편 Modal Analysis Using OptiStruct

안녕하세요. 한국알테어 김정우 선임연구원입니다. OptiSturct 기반의 선형해석 세번째 시간입니다.  Linear Dynamic Analysis 분야에서 가장 기초가 되며 중요한 해석인 Modal Analysis 에 대해서 소개하고자 합니다.

[Eigen Value와 Eigen Vector 의 관계]

일반적으로 물리적 현상에 대하여 수학적으로 표현하면, 많은 경우 고유치 문제로 표현할 수 있습니다. 고유치 혹은 고유값으로 표현되는 이러한 특성은 오늘의 주제와 결부하여 나타내자면 ‘외부에서 어떠한 동적 자극을 받지 않은 상태에서 그 물체가 가지는 본질적인 특성’  즉, 동특성을 의미합니다. 이러한 맥락에서 모드해석을 고유치해석(eigenvalue analysis)이라고도 합니다.

아래 그림의 행렬식이 있습니다.

이 행렬식을 간단히 나타내면 아래  그림처럼 표현됩니다.

여기서 아래와 같은 식으로 성립될 수 있습니다.

위 식의 특성을 살펴보면, 어떤 벡터에 행렬을 곱해도 그 결과값이 기존 벡터의 비율과 똑같다는 것입니다. 이때, 값이 변하지 않는 벡터 x를 eigenvector(고유벡터)라고 부르고, 그 벡터에 곱해져 있는 스칼라 λ를 eigenvalue(고유값)라고 부릅니다.

고유치 해석이라고 하는 부분은 수학적으로 행렬 [A]로 벡터 {x}를 선형변환 (예를 들면, Scaling 또는 Rotation) 시켰을 때, 원래 벡터 {x}의 방향을 가리키는 가중치 λ와 벡터 {x}를 찾는 문제로 설명됩니다. 동적해석의 대상을 예로 들면 고유치는 그 대상의 고유진동수를, 고유백터 {X}는 그 대상의 모드 형상을 각각 의미합니다.

[Modal Analysis 지배방정식]

지난 시간 예로 들었던 일반적인 구조해석에서 사용하는 운동방정식을 다시 한번 보겠습니다.

여기서  는 관성력, 는 감쇠력,  는 탄성력 또는 복원력, 는 외력을 나타냅니다.

Modal Analysis 의 경우, 외력을 받지 않고 감쇠를 무시하며 일체의 비선형성을 고려하지 않는 선형운동방정식을 이용하며, 그 지배방정식은 아래와 같습니다.

로 가정할 수 있습니다. (이 식의 경우 수학자들이 로 가정해서 식을 풀어보니 풀리더라 하여 이 수십년간 가정값을 사용한 것이므로 그렇게 받아들이도록 합니다.) 이러한 가정값을 위의 지배방정식에 대입하면 아래와 같습니다.

위 식에서 ω는 진동수, 는 모드형상을 의미합니다. 위 식은 위에서 설명한 고유치 문제라고 할 수 있으며 그 의미를 조금 더 살펴보자면, 관찰하고자 하는 대상의 관성력  과 탄성력 [K] 이 평형을 이루어 무한하게 진동이 발생하게 됨을 뜻합니다. (왜 무한하게 진동할까요? 감쇠항이 제거되었기 때문입니다.) 이러한 일정한 진동속도가 고유진동수이고, 그때의 진동되는 형상을 모드형상이라고 합니다.

그리고 고유치문제로부터  계산된 ω는 단위가 rad/sec 이므로 Hz 단위의 진동수 (f=ω/2π) 로 변환하여야 합니다.

[Modal Analysis 프로세스]

OptiStruct에서 해석을 진행하기 위한 전처리 프로세스를 살펴보겠습니다. 지난 시간 Linear Static 해석에서의 초기 세가지 단계(1. Geometry Cleanup, 2. 편집된 Geometry 형상에 유한요소 생성하기, 3. 유한요소에 물성 및 속성 정의하여 연결성 부여하기)까지는 동일합니다. 변화가 있는 부분은 그 다음 단계인 하중 및 경계조건 설정부터 입니다. 지배방정식을 통해 유추하시겠지만 하중은 설정하지 않습니다. 경계조건의 경우 설정하는 경우와 설정하지 않는 경우로 나뉠 수 있습니다.

– 경계조건을 설정하는 경우 : 현업에서의 어떠한 시스템이 설치 및 구속된 상태 그대로를 반영하거나, 어셈블리 단위에서 일부 파트만의 동특성을 파악하기 위해 사용됩니다.

– 경계조건을 설정하지 않는 경우 : 부품 단위 혹은 시스템 단위 전체의 동특성을 파악하기 위한 경우로 테스트와의 정합을 진행할 때도 사용됩니다.

하중 및 경계조건 이외에 Modal Analysis 에서는 한가지 필수적으로 쓰이는 EIGRL 이라고 하는 Bulk Data 카드가 있습니다. 아래는 그 설명과 카드 구성입니다.

중요한 내용만 살펴보겠습니다. EIGRL Bulk Data 카드의 3번 필드의 V1은 관심주파수의 시작 주파수, 4번 필드의 V2는 관심주파수의 끝 주파수로 V1, V2는 관심주파수의 범위를 나타냅니다. 5번필드의 ND는 추출되는 모드의 개수를 뜻합니다. 관심주파수에 대한 파악이 되지 않거나 잘 모를 경우에 ND의 모드 개수만 설정해주시면 주파수 범위에 관계없이 ND의 수만큼 고유진동수 추출이 가능합니다.

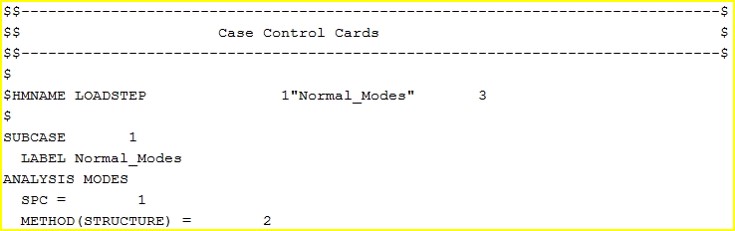
다음 단계로 해석케이스 설정 및 해석수행 부분입니다. Load Step 카드를 생성하여, 그 카드에 해석의 종류를 Normal Modes로 설정, 경계조건이 필요한 경우 SPC 란에 Assign, EIGRL 카드는 METHOD (STRUCTURE) 란에 Assign 해주시면 해석에 대한 전처리가 완료됩니다. 아래 그림은 해당 설정을 완료한 INPUT 파일 내용입니다.

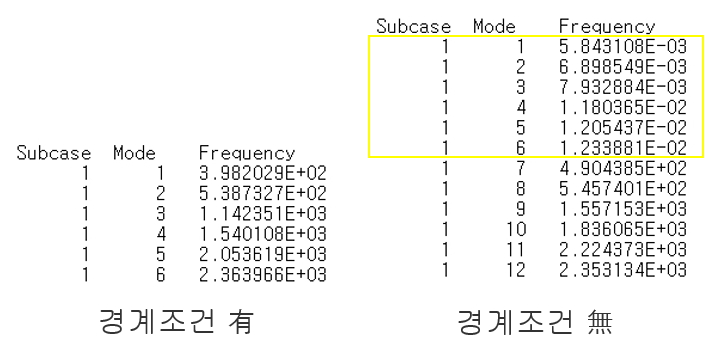
그렇게 해석을 진행한 후 결과는 HyperView를 통해 각 모드마다의 모드형상을 애니메이션으로 확인하실 수 있습니다. 또한 각 모드의 주파수만 확인하고자 하는 경우에는 아래 그림과 같이 *.out 파일을 문서편집기로 열어 간단히 확인하실 수 있습니다.

[Rigid Body Mode]

위 그림의 오른쪽의 해석결과를 살펴보면 경계조건이 없는 상태에서는 1차부터 6차까지 변형이 없이 진동수가 0Hz에 가까운 상태의 Mode가 있음을 확인할 수 있습니다. 이를 Rigid Body Mode라고 하며, 일반적인 3차원 모델은 X, Y, Z축 방향으로의 병진이동모드(translation) 3개와 회전모드(rotation) 3개, 총 6개의 Rigid Body Mode를 갖습니다. 이에 따라 1차 모드부터 6차 모드까지 Rigid Body Mode가 발생하고, 이후 7차모드부터 변형에너지가 발생하는  진동모드로 간주하게 됩니다.

[결과분석]

해석의 결과로 추출된 모드 중 저차모드에 해당되는 몇 개의 모드의 주파수가 어떠한 시스템의 작동주파수의 범위에 있게 되면, 공진발생의 가능성이 높기 때문에 이를 회피하도록 설계 변경을 해야합니다. 고유진동수(f)는 구조물에 강성(k)에 비례하고 질량(m)에 반비례하는 특성이 있기 때문에 모드 형상 또는 변형에너지 측면에서 판단하여 구조물의 강성과 질량을 조절해가며 설계에 반영하도록 합니다. 일반적으로 구조물의 고유진동수가 작동주파수 대비 1/3 이하 또는 3배 이상의 범위에 있도록 하는 것이 안전한 설계라고 할 수 있습니다.

지금까지 세 차례의 연재로 인사를 드렸습니다. 짧은 분량으로 Linear Static Analysis와 Modal Analysis에 대한 내용을 모두 파악하는 것은 무리가 있습니다만 CAE 분야에 막 발을 내딛게 된 초심자분들에게는 유용한 연재가 되었기를 소망해봅니다. 다음 연재부터는 YUNA 연구원이 연재를 재개할 예정이니 많은 기대 부탁드립니다.

– 참조
이 자료는 “Practical Finite Element Analysis” 책의 내용과, HyperWorks Help Documentation 자료를 포함하고 있습니다.
© 2015 Altair Engineering, Inc. All rights reserved. No part of this publication may be reproduced, transmitted,transcribed, or translated to another language without the written permission of Altair