야금야금 CAE: 꿀바른 HyperWorks (제 5편 FEA 소개)

한국알테어의 YUNA 입니다!
유한요소해석에 관심있는 모든 분들을 위해 간단한 이론과 HyperMesh를 이용해서 FEA Process를 차근차근 배워보는 “야금야금 CAE: 꿀바른 HyperWorks”를 연재합니다.
1년에 걸쳐 연재할 예정이니 앞으로 한 주에 하나씩 함께 배워요!

제 5편 FEA(Finite Element Analysis) 소개

한 주 동안 잘 보내셨나요? 이번 편은 FEA 초보자분들이 읽고 ‘뭔가 알 것 같은 느낌?!’ 을 만들어 드리는 데 주력해보고자 합니다! FEA(Finite element analysis)는 공학분석에 사용되는 컴퓨터 시뮬레이션 전체 과정을 말하며, FEM라고 불리는 수치적 기법을 사용하여 답을 찾아나갑니다!

(1) 공학적인 문제를 풀기 위한 방법?

해당 방법에는 대표적으로 3가지가 있습니다.
1.Analytical Method
구조물의 기하학적 형상을 이용해서 문제를 푸는 고전적인 방법입니다.
2.Numerical Method
컴퓨터를 통해 수학적인 방법으로 시뮬레이션을 해서 값을 구하는 방법입니다.
3.Experimental Method는 실제 실험을 통해 값을 구하는 방법입니다.
우리가 관심있는 FEM은 Numerical Method 안에 속해있으며, Numerical Method부터 하나씩 살펴보겠습니다.

(2) Numerical Method

1.Finite Element Method (FEM) – 유한요소법
FEM은 가장 대중적으로 쓰이는 numerical method중 하나입니다. FEM은 구조물을 서로 연결된 유한개의 element(요소)로 분할 후 node(모서리)에서 계산하여 전체 구조물을 계산하는 방법입니다.
2.Boundary Element Method (BEM) – 경계요소법
BEM 기법 또한 FEM처럼 element를 필요로 하지만, 오직 구조물의 경계조건만을 고려하는 방법입니다. 만약 공학적인 문제가 체적(volume)을 다루고 있다면, 오직 바깥면의 surface만 고려합니다.
3.Finite Volume Method (FVM) – 유한체적법
FVM은 유한개의 체적으로 분할하여 계산하며,  FEM과는 다르게 체적의 중앙을 계산합니다.
4.Finite Difference Method (FDM) – 유한차분법
FDM은 FEM과 유사하지만, FDM은 미분 방정식에 대해 근사화하고, FEM은 미분 방정식의 해법에 대해 근사화 한다는 점이 다릅니다.

(3) FEM에서 Meshing 이란?

실제 모든 물체는 연속적입니다. 이어진 입자 사이에 물리적인 틈이 없다는 말이죠. 하지만 공학적인 문제를 연속적인 물체로 간주해서 푸는 것은 매우 어려운 일입니다. FEM에서는 구조물을 컴퓨터가 계산할 수 있도록, meshing을 통해 이산화를 해줍니다. 즉, 유한개의 elements로 분할해 주는 것이죠.

(4) DOF란?

Degrees of freedom의 약어로 DOF, 혹은 자유도라고 합니다. 시스템의 자유도란, 독립적으로 달라질 수 있는 정도를 말하는데요, 역학에서 자유도란 바디가 움직일 수 있는 독립적인 운동의 수입니다. 예를 들어보면, 1차원상의 직선 방향으로만 움직이는 자동차는 1개의 자유도를 가질 것입니다 위치가 트랙을 따른 길이에 의해서 정의되기 때문입니다.
2차원상에서, x, y 평면이라면, 자동차는 두 개의 직선운동 요소와 회전운동으로 구성된 3개의 독립적인 자유도를 갖습니다. 3차원 공간의 비행기를 예로 들면, x,y,z방향 직선운동과 각 축 방향으로의 회전까지 총 6개의 자유도를 갖습니다. FEM에서는 각각의 node에서 자유도를 계산하게 됩니다. 전체 DOF의 수는 전체 노드에 각 노드가 가진 자유도의 수를 곱해서 모든 항을 더하면 됩니다.

(5) FEM의 stiffness란?

Stiffness(강성) ‘K’ 란 힘/길이로 변위에 저항하는 성질이라고 생각하면 됩니다. 강성은 형상에 따라 달라지며, 재료 특성에도 의존합니다. 아래와 같이 동일한 형상의 기둥에, 동일한 F를 적용한다면, K값은, 주철 > 연강 > 알루미늄 순서로 나타날 것입니다.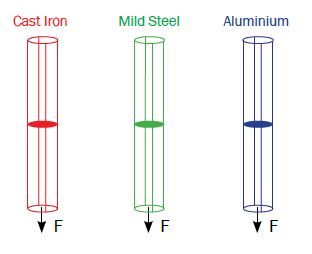

(6) stiffness matrix 를 푸는 방법?

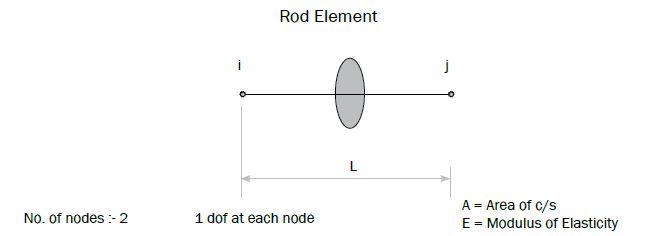
Direct Method (직접법), Variational Method (변분법), Weighted Residual Method (가중잔여법)이 있습니다. 가장 직관적으로 이해가 쉬운 Direct Method로 간단한 1D 외팔보의 [F]=K[U] 식을 유도해 보겠습니다. node는 양 끝 단에 2개(i 노드, j 노드) , 전체 길이는 L, 면적은 A, 탄성 계수는 E 이며, 각각 노드가 가진 자유도는 1입니다.
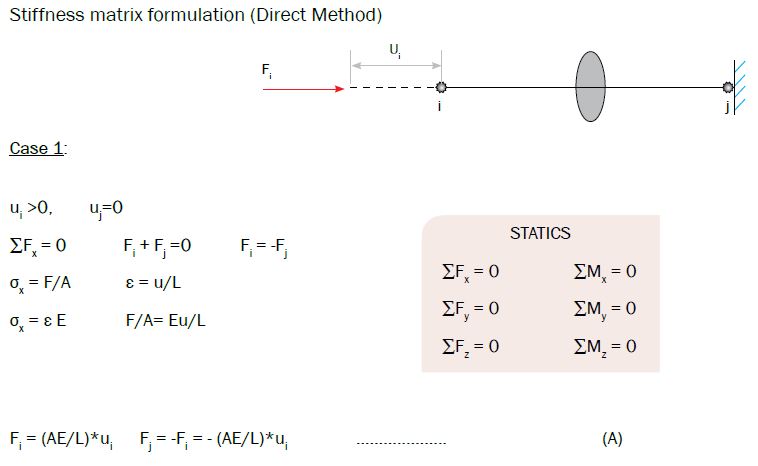이렇게 얻은 두 개의 수식을 Matrix 형태로 표현해주면 아래와 같은 형태를 얻을 수 있습니다.

Direct Method는 직관적으로 이해하기는 쉽지만, 프로그래밍이 어려우므로, 프로그래밍이 쉬운 Variational Method, Weighted Residual Method를 사용하게 되고, 복잡한 계산은 Solver가 해줍니다. 이번장에서는 FEM의 용어들과, ‘각 Node에서 계산해서 풀어나가는구나~’ 를 기억해주시면 좋을 것 같습니다!

이번 블로그는 여기까지입니다. 다음 시간에는 FEA를 위해 필요한 것이 무엇인지 살펴보도록 하겠습니다. 다음 시간에 만나요~

– 참조
이 자료는 “Practical Finite Element Analysis” 책의 내용과,  HyperWorks Help Documentation 자료를 포함하고 있습니다.
© 2015 Altair Engineering, Inc. All rights reserved. No part of this publication may be reproduced, transmitted,transcribed, or translated to another language without the written permission of Altair