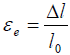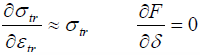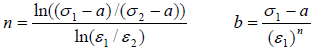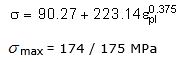RADIOSS Example 공략 11편 – Tensile Test (Law Characterization)

목적

이번 예제의 목적은 시편 인장시험의 실험 값을 RADIOSS에서 제공하는 다양한 재료를 사용하여 비교해보는 것입니다. 사용된 키워드는 LAW2, LAW27, LAW36으로 탄소성 물성에 사용되는 키워드들입니다. 비교를 위해 공칭(engineering), 진(true) 응력-변형률 선도를 사용했으며 실험 결과와 더욱 잘 매칭시키기 위해서 데미지와 파괴 모델 또한 적용되었습니다.

---

모델 정보(Geometry)

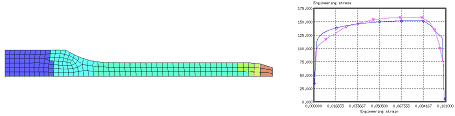
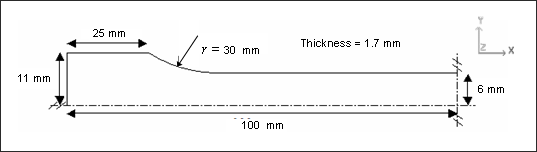
모델의 왼쪽 끝에 강제 속력을 부여하고, 1/4의 대칭조건으로 해석을 진행했습니다. 실험에서 사용된 재료는 6063 T7 Aluminum입니다.

물성 정보 (Material)

단위 :  mm, ms,  g, N, MPa

재료는 등방 탄소성 거동을 보이기 때문에 RADIOSS에서는 Johnson-Cook 모델에 대미지를 적용한 것과 적용하지 않은 것(각각 LAW27, LAW2) 그리고 table로 소성 영역을 정의하는 LAW36번을 사용하여 실험 값과 결과를 비교 할 수 있습니다.

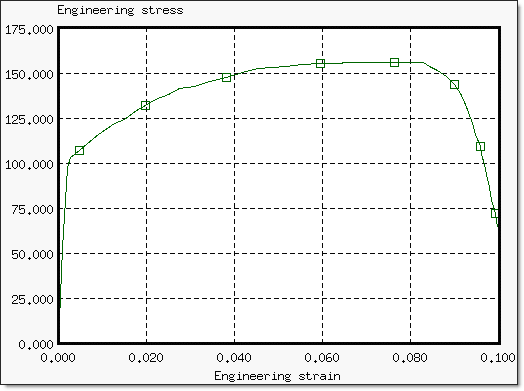
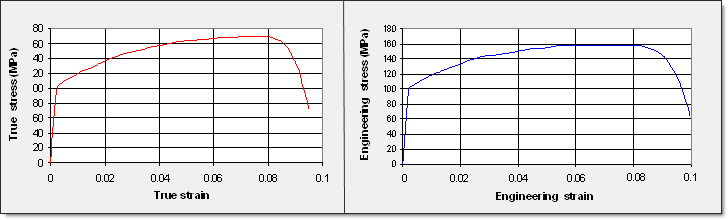
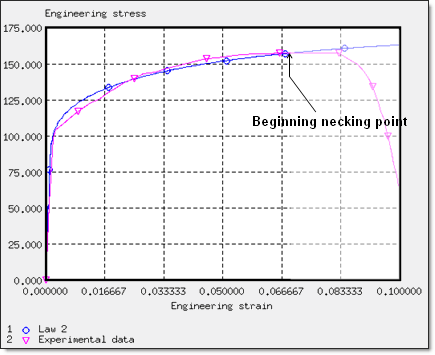
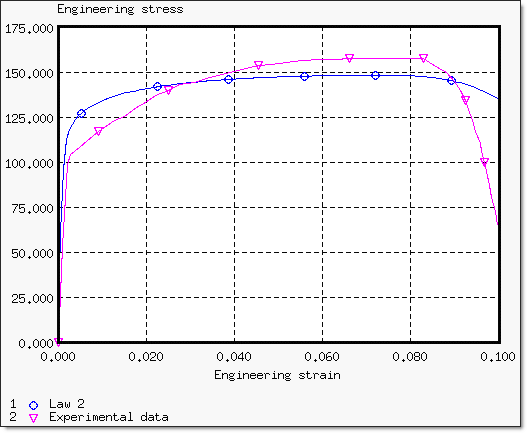
위 그림은 시편 인장 시험의 실험 결과로 공칭응력 공칭변형률로 표현된 S-S커브입니다.

모델링 정보

요소의 평균 사이즈는 2mm로 201개의 4-node shell 요소와 1개의 3-node 쉘이 사용되었습니다. 그 외 적용된 쉘 property 옵션은 다음과 같습니다.

– 5 integration points (progressive plastification).
– Belytschko elasto-plastic hourglass formulation (Ishell = 3).
– Iterative plasticity for plane stress (Newton-Raphson method; Iplas = 1).
– Thickness changes are taken into account in stress computation (Ithick = 1).
– Initial thickness is uniform, equal to 1.7 mm.

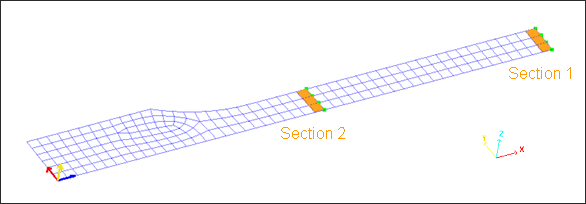
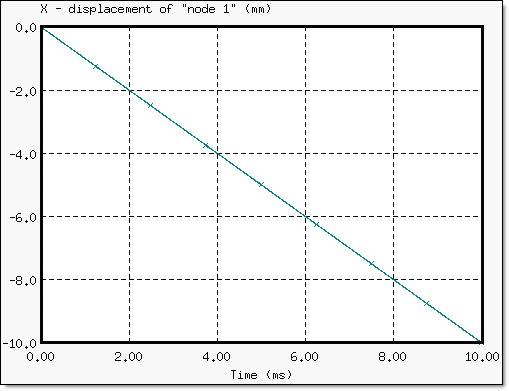
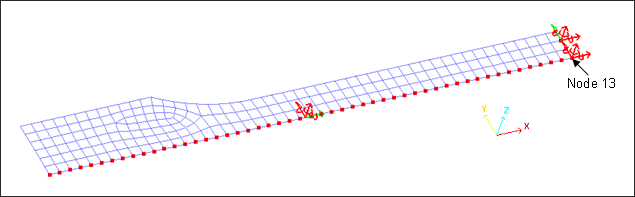
위 그림에 보이는 Node 1은 Node 54번이었으나 해당 노드에서 그래프 데이터를 추출하기 위해 이름을 변경했습니다. 이 위치에서 x축 방향의 변위가 기록됩니다.

또한 Section을 설정하여 해당 부분에서 발생하는 Force를 그래프 데이터로 추출 할 수 있습니다.

RADIOSS에서 Output을 설정하는 방법은 아래 블로그 를 참조하시기 바랍니다.
팁 : Section의 Time History 추출 방법  http://blog.altair.co.kr/26556

경계 조건 설정 (Boundary Conditions)

그림에 보이는 녹색 Node들에 강제 속도를 부여했으며 이들은 각각 1m/s입니다. X축 방향의 반대 방향이므로 정확하게는 -1m/s가 입력되었습니다.

1/4 대칭 모델임을 시뮬레이션 상에서 표현하기 위해 빨간색 Node들에 구속조건을 설정했습니다.

재료 특성 묘사 (관계식 정의)

재료의 거동 특성을 묘사하기 위한 방법은 아래 두 가지가 있습니다.

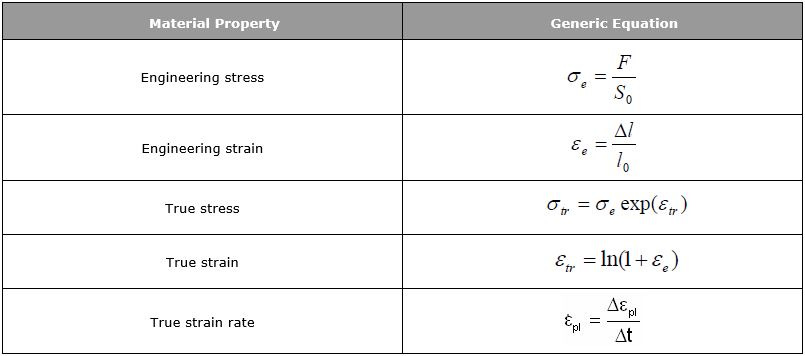
1. 공칭응력-변형률 커브를 진응력-변형률 커브로 변환하는 방법 (어떠한 Material에도 적용 가능한 방법)

2. 진응력-변형률 커브에서 주요 인자들을 추출하여 물성의 거동을 정의하는 방법(Johnson-Cook 물성인 LAW2와 LAW36에 가능)

공칭응력은 아래와 같은 계산식으로 계산 할 수 있으며,

진변형률은 아래 관계식으로 계산됩니다.

진변형률, 공칭변형률 둘은 아래와 같은 관계식으로 엮여있어 둘 중 하나의 값을 알면 쉽게 구할 수 있습니다.

공칭응력은 초기 면적으로 계산되어지지만, 진응력은 변형되어지는 면적들로 각각 계산되어집니다.

이와 같이 진응력을 계산시 면적의 변화를 반드시 고려해야 하며 포아송비가 0.5인 경우에 소성변형을 가정하면 단축방향의 표면적은 다음과 같이 고려 할 수 있습니다.

결론적으로 공칭응력과 진응력과의 관계는 아래 관계식으로 정의 할 수 있습니다.

 

재료 특성 묘사 (인풋 모델 구성)

RADIOSS에서 해당 물성을 묘사하기 위해서 LAW2, LAW27, LAW36이 사용되며 각각의 물성에서 항복응력과 영률은 커브로부터 계산되어집니다.

소성 변형률은 다음과 같이 구할 수 있으며,

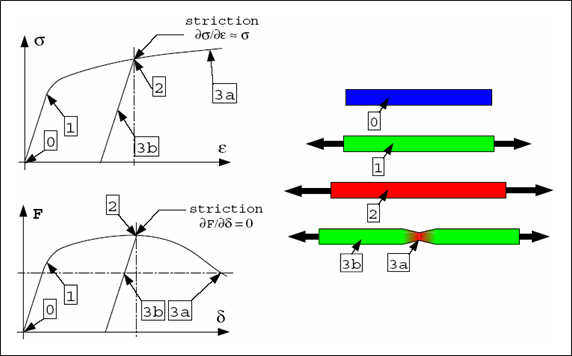
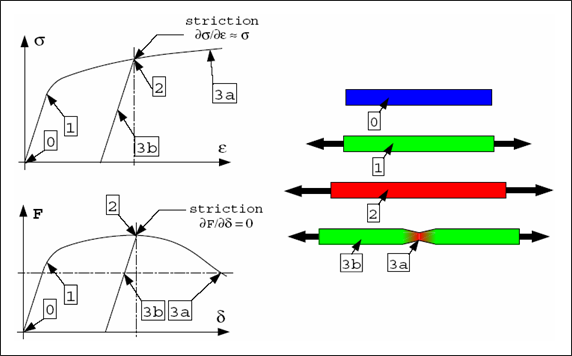
물성 묘사에 중요한 점은 necking point(네킹점)으로 Force – Displacement 커브의 기울기가 0이되는 지점입니다. 이에 대한 관계식은 아래와 같습니다.

 

 

실험 결과
인장 시편 시험은 “Norwegian Institute of Technology”의 EC-fianced program의 일부인 “Calibration of Impact Rigs for Dynamic Crash Testing”이 사용되었습니다. 아래 커브는 실험의 결과입니다.

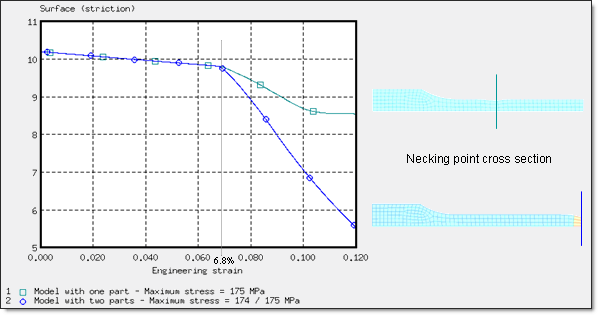
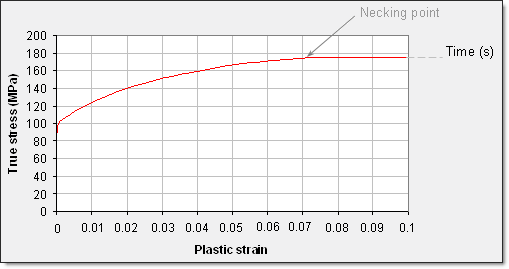
결과를 분석하면 nekcing point는 변형률이 6% ~ 8%구간 (공칭변형률)에서 발생하는 것을 확인 할 수 있습니다. 정확하게는 6.68%입니다.

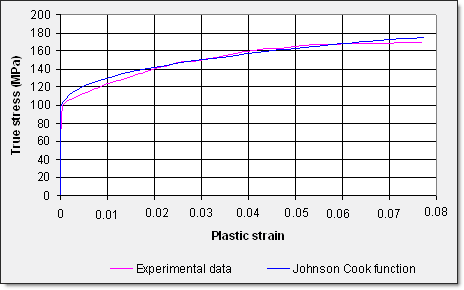
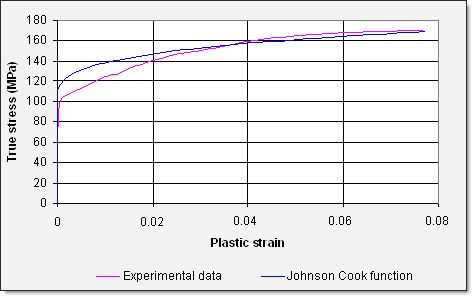
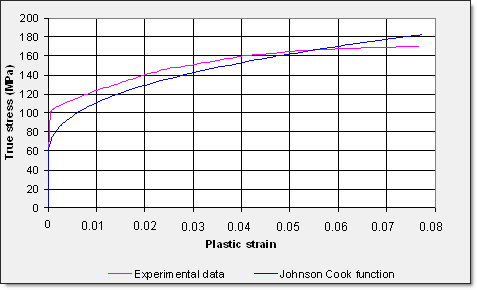
진응력 커브는 시편의 단면이 줄어듬을 고려하기 때문에 공칭응력 커브에 비해 높은 변형률 값을 나타내고 있습니다.

Law 2 : Johnson-Cook 물성을 이용한 탄소성 재료 시뮬레이션
Johnson-Cook 모델에서 응력과 변형률의 관계는 다음과 같습니다.

Law2에서는 소성영역의 값을 상수로 결정합니다. 이에 필요한 값으로 n과 b가 있으며 이들은 항복응력과 공칭응력,변형률을 진응력, 변형률로 변환 후 아래 관계식으로 구할 수 있습니다.

Johnson-Cook의 변수들을 처음 결정하는 단계에서는 최대 응력 또는 최대 소성변형률은 고려되지 않으며(0으로 설정됨), 값들이 선택된 후에 실험 결과에 맞추게 됩니다.

처음 네킹점이 선택되면 b와 n은 각각의 커브 위치의 값으로 계산 할 수 있습니다. 그리고 이 값들을 평균하게되는데 이는 선택된 네킹점에 따라서 결과가 다를 수 있기 때문입니다.

따라서 이들을 이용하여 Law2에 입력 할 값들을 다음과 같이 구할 수 있습니다.

Initial density : 2.7×10-3 g/mm3
Yield stress : 90.27 MPa
Poisson’s ratio : 0.33
Hardening parameter : 223.14 MPa
Young’s modulus : 60400 MPa
Hardening exponent : 0.375

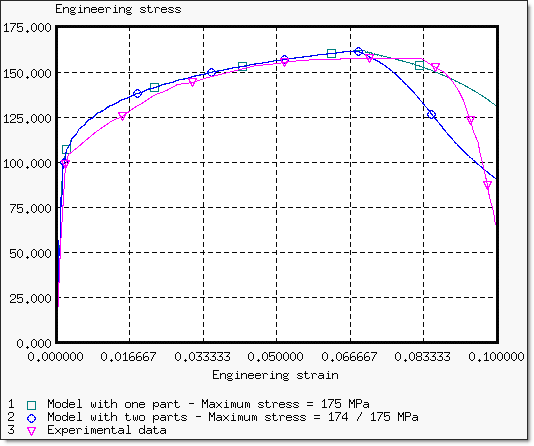
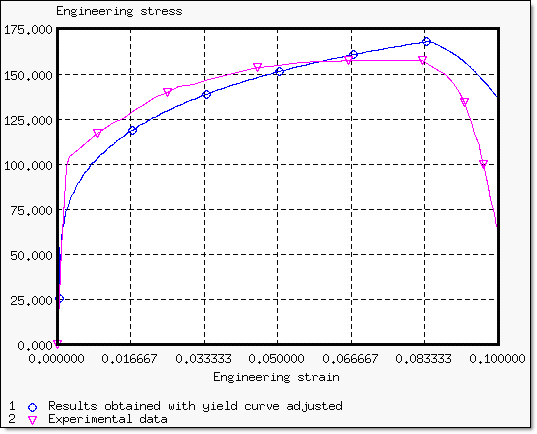
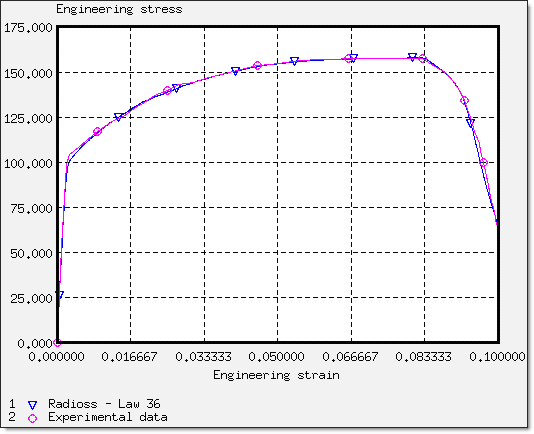
이렇게 구한 값들을 커브로 그렸을 때 아래와 같으며 실험결과와 같이 비교했습니다.

진응력-변형률 관계는 아래 식으로 구했으며,

다음 표는 실험과 시뮬레이션의 공칭응력 결과의 차이를 나타내고 있습니다.

네킹점이 6.68% 이후에는 공칭 응력이 가파르게 감소하기 때문에 네킹점 이전을 기준으로 비교했습니다.

네킹시작 점 분석
Johnson-Cook 모델로 네킹점까지의 실험 값과 결과를 맞춰왔지만, 다수의 응답들의 기울기로 네킹이 시작되는 지점을 정확하게 일치시킬수는 없습니다.

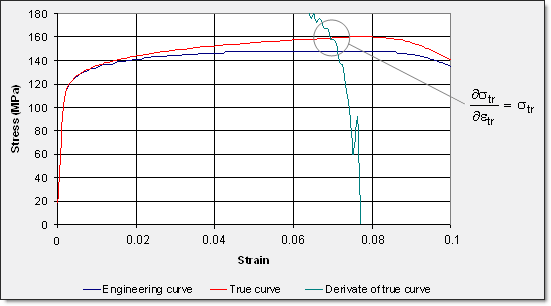
네킹점은 진응력-변형률 선도의 기울기로 부터 묘사되었지만, 정확한 네킹점을 묘사하기 위해서는 여전히 변수의 조정이 필요합니다.

 

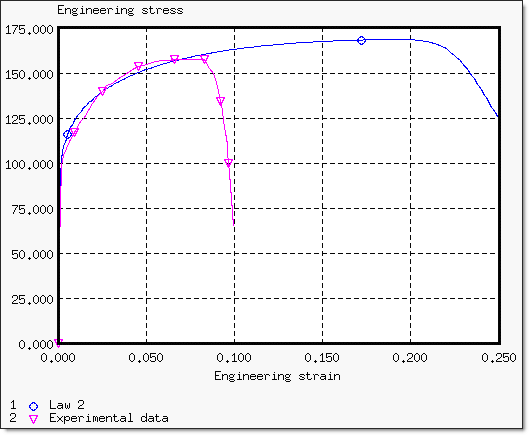
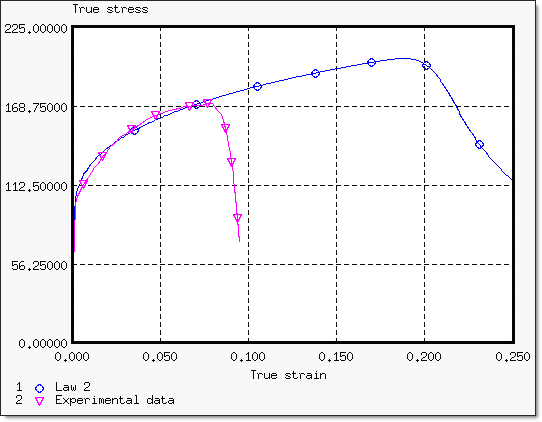
a, b, n 같은 변수를 사용했을 때의 결과입니다. (공칭, 진)

네킹점을 조절하여 피팅하기 위해서는 a, b, n 값들을 조절하는 방법 또는 최대응력 값을 맞추는 방법이 있습니다.

네킹점 부근에서의 기울기 시뮬레이션

에너지적 접근을 구현하는 것으로부터 하드닝 커브를 공칭커브에 맞게 수정 할 수 있습니다.

물리적 기울기를 묘사하기 위해서 사용한 Johnson-Cook 값들은 아래와 같습니다.

Yield stress : 79 MPa
Hardening parameter : 133 MPa
Hardening exponent : 0.17

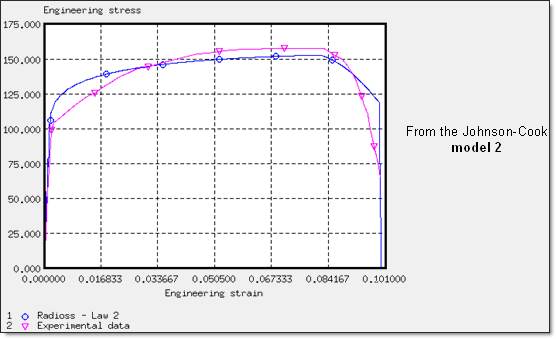
이 모델에 대해서 새로운 진응력-변형률 관계식이 적용되었고 이는 Johnson-Cook 모델 2로 명명하겠습니다.

결과는 아래 그림과 같습니다.

항복에 대한 커브를 실험 값과 비교한 그래프입니다.

네킹점은 다음과 같이 정의되며 이 조건은 진응력-변형률 선도의 교차로 부터 묘사됩니다.

 

최대 응력 값 제한 방법을 이용한 네킹 시작점 고찰

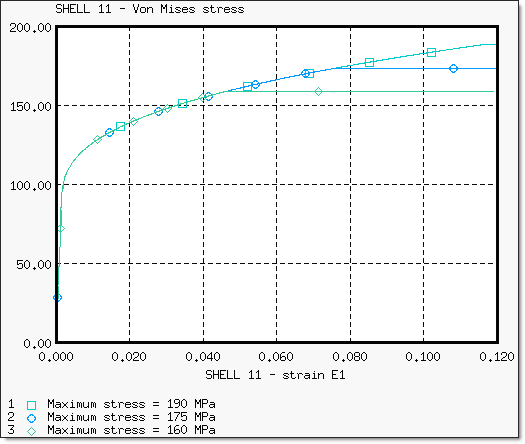
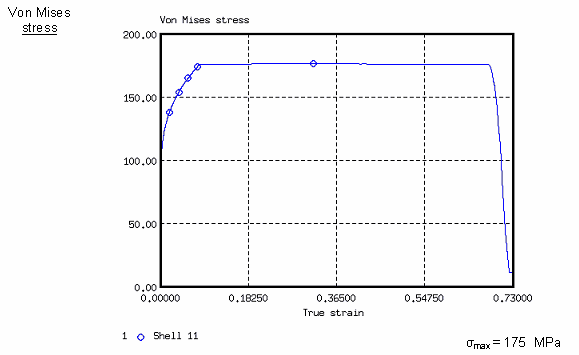
이번 시험에 대해서 Johnson-Cook 인풋 값들은 네킹점까지의 묘사를 위해 설정되었습니다. 파손은 고려되어지지 않은 모델입니다. (파손 소성 변형률은 0으로 설정) 아래 표를 보면 최대 응력이 175MPa일때의 네킹점이 실험값과 가장 유사한 것을 알 수 있습니다. 이는 곧 최대 진응력으로 인해 네킹이 시작되는 것을 조절 할 수 있다는 것을 알 수 있습니다.

shell11번에 대한 본미세스 응력 값 비교 그래프

 

최대 응력은 네킹이 시작되는 부분에서 가장 높은 본미세스 응력 값을 나타냅니다. 네킹 후에 응력값이 높아지는 것을 피하기 위해서 최대 응력의 값은 반드시 네킹지점의 진응력 값과 일치시켜야 합니다.

아래 보이는 커브는 시편의 변화에 따라 본미세스 응력과 진변형률 선도의 양상을 보여주고 있습니다.

아래 그림을 보면 네킹이 시작되는 때는 기울기가 다음 관계식과 일치하는 때라는 것을 볼 수 있습니다.    

항복 선도는 다음과 같이 표현 할 수 있습니다.

응력의 유도는 항복선도 정의에 따라서 매우 민감하고 강하게 의존되기 때문에 시뮬레이션으로 네킹점을 도입하는 것은 매우 민감한 문제입니다. (작은 변화에도 값이 상당히 다를 수 있기 때문에) 그래서 주어진 요소에 대해서 네킹점은 반드시 먼저 시작되어야 합니다. 바람직한 네킹의 시작점은 아래 설명하도록 하겠습니다.

 

바람직한 네킹 시작점 분석

실험적으로 네킹이 시작되는 위치는 정확하게 예측하기 어렵습니다. (어디서도 발생 할 수 있기 때문) 본 예제에서는 네킹이 반드시 오른쪽 끝 요소에서 발생해야 합니다. 만약에 모델이 1/4로 사용되었다면 네킹은 요소 30, 125 그리고 78번에서 발생 할 것입니다.

네킹의 시작은 물리적으로나 수치적으로 민감하고 오른쪽 끝에 위치한 일부 요소들의 노드 위치를 변경하는 것으로 부터 네킹을 유도 할 수 있습니다. 본 모델에서는 가장 오른쪽 노드의 위치를 0.01mm 이동하는 것 만으로도 충분히 네킹을 유도 할 수 있습니다.

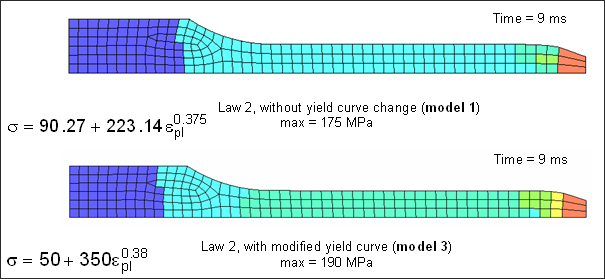
두번째 접근은 오른쪽 끝부분을 추가적인 파트로 분리하여 강제적으로 네킹이 시작되게 하는 것입니다. 네킹을 국부적으로 발생시키기 위해서 쉘 3, 11, 4번이 포함된 파트의 최대 응력 값을 남아있는 파트보다 더 작은 최대 응력 값을 설정해주게 됩니다. 이러한 방법은 재료의 특성에 기반하기 때문에 꽤나 정확하게 재료의 특성이 묘사 할 수 있습니다.

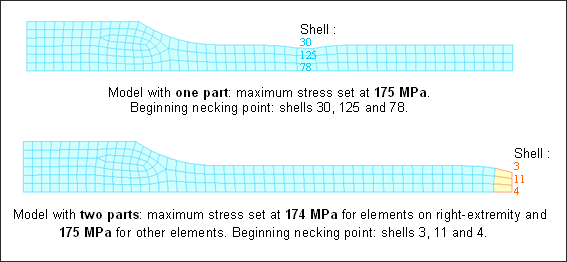
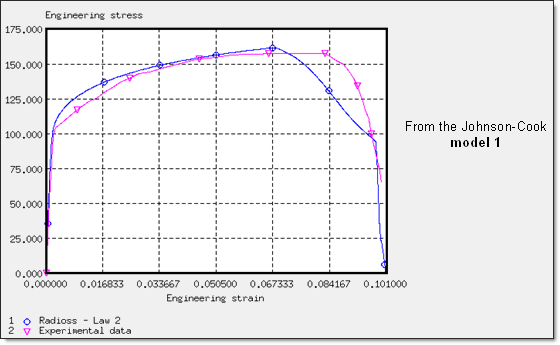
본 모델에서 사용된 재료 특성은 Johnson-Cook model 1과 같습니다.

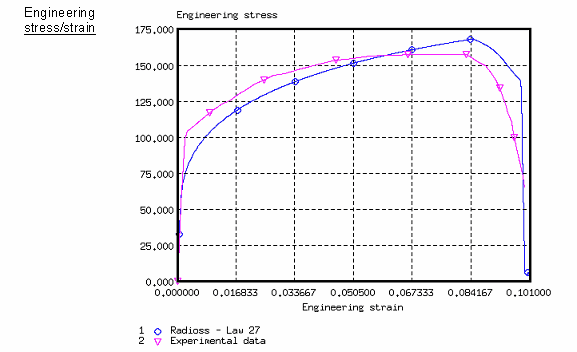
아래 보이는 커브는 공칭응력-변형률 선도로 기존 방법, 네킹을 유도한 방법, 그리고 실험 값과의 결과를 비교한 것입니다.

오른쪽 끝 부분에서 네킹이 시작되면 공칭응력은 가파르게 감소하게 됩니다. y축 대칭평면의 구속 조건 때문에 네킹점은 좀 더 확연하게 나타나게 됩니다.

기존 모델과 파트를 두개로 나눈 모델의 결과를 비교해보면 네킹이 시작기 전까지는 거의 동일한 경향을 보이나, 네킹이 시작된 후에 경향이 확연하게 다른 것을 볼 수 있습니다.

 

네킹이 진행되는 동안 요소의 힘 전달 개선 (요소간 에너지 전달)

네킹점에서 각각의 요소가 물리적으로 거동하는것을 시뮬레이션 하기 위해서는 Johnson-Cook 변수들을 다양하게 조절해야 할 필요가 있습니다. 최종 결과는 더 이상 응력-변형률 선도를 조절하지 않지만 시험 동안의 에너지 분산을 묘사하는 것은 중요합니다. 이 같은 에너지 기반의 접근은 결과를 어떻게 도출했는지 보다 마지막 평가가 더욱 중요하기 때문에 충돌시험에서 매우 중요하게 생각합니다.

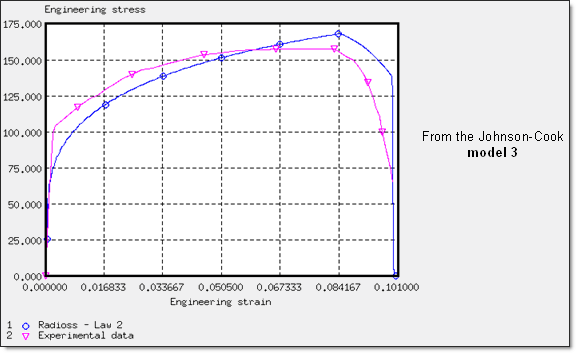
위 그림은 Johnson-Cook 변수들을 조절하여 얻은 공칭응력-변형률 선도입니다.

다음은 항복 선도입니다.

해석에 사용된 Johnson-Cook 변수들은 아래와 같으며 이는 model 3으로 명명됩니다.

 (진응력/진변형률)

Yield stress = 50 MPa
Hardening parameter = 350 MPa
Hardening exponent = 0.38
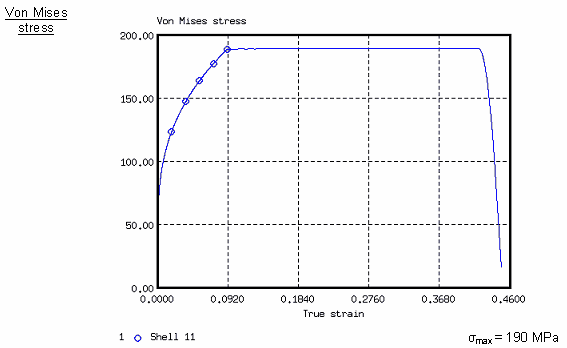
Maximum stress is set to 189 or 190 MPa (네킹점이 작은 응력)

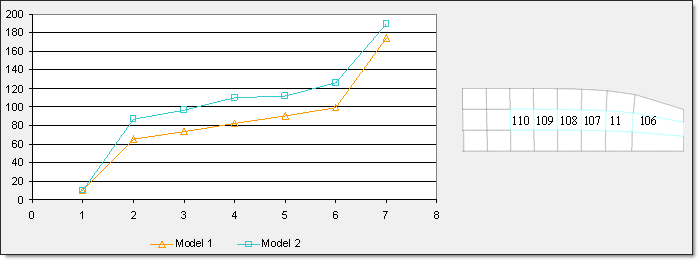
아래는 모델 1과 모델3의결과를 비교한 그림입니다.

네킹점이 진행되는 것 처럼, 새로운 모델이 더 고른 에너지 전달을 보이게 되어 보다 현실적이고 물리적인 결과들을 얻을 수 있었습니다.

위 그림은 쉘 요소 110, 109, 108, 107, 11, 106번에 대한 본미세스 응력 값을 나타내고 있습니다.

 

데미지 & 파손 옵션 적용

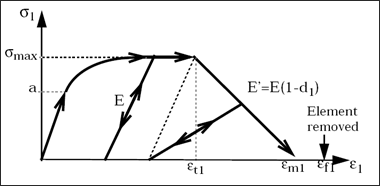
탄소성 모델은 파손 직전까지 사용됩니다. 데미지 및 파손 옵션을 적용하게 되면 요소가 소성영역에 접근하게 됐을 때(입실론 max값) 제거되게 됩니다. 이러한 데미지 모델은 매우 좋고 안정적인 결과를 보여주게 됩니다.

다음 그림은 최대 소성 변형률이 적용된 Johnson-Cook 모델1 입니다.

입실론 max 값이 75%인 경우 모델1

입실론 max 값이 47%인 경우 모델2

입실론 max 값이 40%인 경우 모델3

위 결과들 각각 파손은 매우 높은 변형률 상태에서 발생했습니다.

 

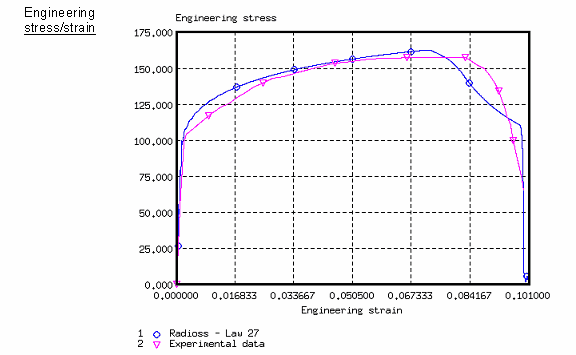
Law 27 : 데미지 옵션이 적용된 탄소성 물성

Law27은 Johnson-Cook의 소성성을 데미지 옵션을 적용하여 시뮬레이션 하기 위한 물성입니다.

데미지 파라미터들은 다음과 같습니다.

– Tensile rupture strain 입실론t1 : 가장 높은 변형률 값이 이 값에 도달하면 데미지 옵션이 적용됩니다.

– Maximum strain 입실론m1 : 가장 높은 변형률 값이 이 인장 값을 넘게되면 요소에 데미지 옵션이 적용되지만 요소는 제거되지 않습니다.

– Maximum damage factors 시그마max: 이 값은 기본 값으로 유지되야 합니다. (0.999)

– Failure strain 입실론f1 : 가장 높은 변형률 값이 인 값에 도달하면 요소가 제거됩니다.

 

데미지 옵션에 영향을 받는 응력-변형률 선도에 대한 그림입니다.

아래 보이는 그래프들은 데미지 옵션이 적용된 모델의 결과를 실험 값과 비교한 것입니다.

 

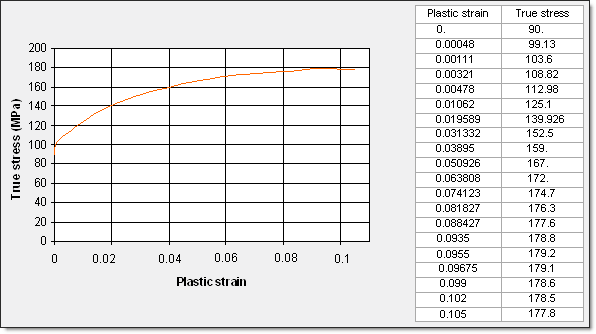
Law 36 : 테이블로 표현하는 탄소성 물성

테이블로 소성영역을 정의하는 Law36 물성을 사용하여 진응력 – 소성변형률의 값이 적용되었습니다. 이러한 Hardening 함수를 추가하여 파손 역시 시뮬레이션 가능합니다.

실제 실험 결과와 하드닝 커브를 일치시키는 것은 매우 미세하고, 민감한 작업이므로 소수점까지 정의해야 합니다. 네킹부의 결과를 좀 더 좋게 하기 위해서 몇몇 구간들의(네킹전과 후) 값들은 보간했습니다.
결론

위의 결과들을 종합해서 보면 Law 36을 사용하여 소성영역의 값을 정확하게 정의해주는 것이 가장 좋은 결과를 얻을 수 있으며 이렇게 많은 정보가 없는 경우 Law2, Law27을 사용하여 근사한 결과를 얻을 수 있음을 확인했습니다. 좀 더 정확하게 결과를 얻기 위해 데미지옵션을 적용하거나 강제로 네킹부를 정할 수 있는 모델링 기법들에 대해서도 언급이 된 예제입니다. 실로 모델링 하는 것은 간단하지만 모델링 하나 하나에 숨어있는 뜻을 알아보는 성격이 강한 예제였습니다.

끝.

공략 12편 – Jumping Bicyle

<-- 이전 글 보기

다음 글 보기 –>