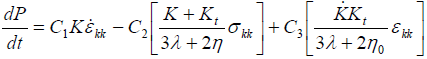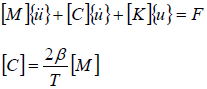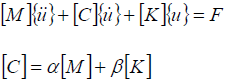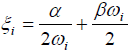목적
본 예제의 목적은 Kinetic relaxation, Dynamic relaxation 그리고 Rayleigh damping이 고려된 준정적 하중을 다루는 것입니다. 이러한 3가지 다른 접근이 고려된 explicit 해석을 비교 분석 할 계획입니다.
물리적 문제 정의
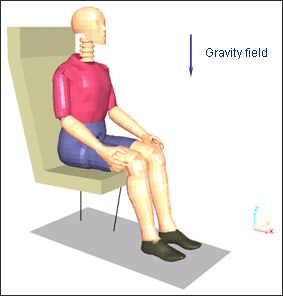
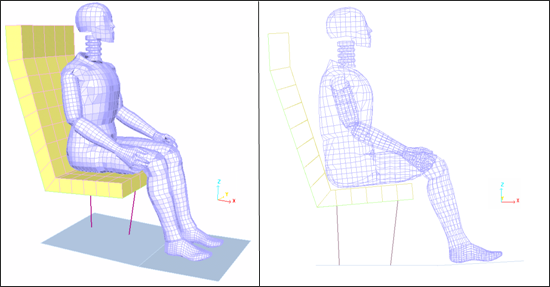
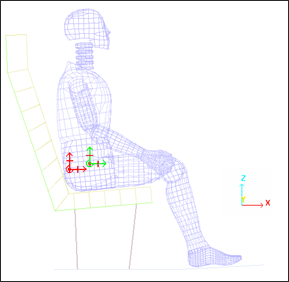
동적 충격 시뮬레이션에 앞서서 중력장의 영향을 받는 더미를 의자에 안정화 시키는 과정을 준정적 접근으로 진행합니다.
더미의 무게는 80kg이며 (173.4 파운드) 전체적인 더미의 무게만 고려됩니다. 시뮬레이션 결과에 영향을 주지 않기 위해 물성은 간력하게 묘사하고 중력 하중에 의해 더미의 변형은 발생하지 않도록 설정합니다.
설정한 물성은 다음과 같습니다.
시트 지지대 물성 – 하부의 기둥 (/MAT/LAW1)
– Young’s modulus : 210000 MPa
– Poisson’s ratio : 0.3
– Density : 7.8 x 10-9 Gkg/I
시트 특성
– Area : 2580 mm^2
– Inertia : Ixx = 554957 mm^4 , Iyy = 554975 mm^4 , Izz = 937908 mm^4
시트 뒷편
– Brace thickness : 2 mm
– Floor thickness : 1 mm
시트 쿠션은 폼재질로 구성되어 있으며 Kelvin-Voigt 모델이 적용되었습니다. 물성은 다음과 같습니다.
– Young’s modulus : 0.2 MPa
– Poisson’s ratio : 0
– Density : 4.3 x 10-11 Gkg/I
– E1 , E2 : 0 MPa
– Tangent modulus : 0.25 MPa
– Viscosity in pure shear : 10000 MPa/s
– C1 = C2 = C3 = 1 (visco-elastic bulk viscosity)
RADIOSS 물성 Law35번이 사용되었으며 cell foam option은 활성화 시키지 않습니다. (Iflag=0) 그리고 압력은 아래 테이블과 같이 커브로 적용됩니다.
테이블 1 : 압력 압축 커브
점탄성폼 재질 (/MAT/LAW35)
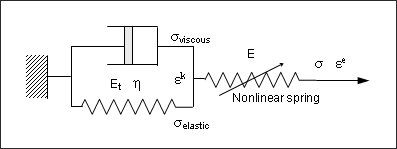
나비에 방정식에 기반한 Law 35는 점탄성 거동의 물성을 묘사합니다. 닫혀져 있는 공기의 영향을 압력-압축 선도를 통해서 고려됩니다. 완화 (Relaxation)과 크립 (creep) 역시 모델링 할 수 있습니다. 아래 그림의 예시는 일반화된 Kelvin-Voigt 모델을 묘사하고 있습니다.
두 압력 계산들은 open cell을 갖고 있지 않은 폼에 대해 RADIOSS에서 이용가능합니다.
아래는 기본으로 사용된 수식입니다.
압력 은 사용자가 정의한 압력-압축 선도를 이용하여 계산되며, 압축은 다음과 같이 표현 가능합니다.
여기서 p는 시간 t에서의 밀도이며 p0는 초기 밀도입니다.
분석과 가정 그리고 모델링 묘사
모델링 기법
모델은 두개의 서브셋으로 구성되어 있습니다.
- 38개의 파트로 구성된 더미 (림프와 조인트)
- 6개의 파트로 구성된 시트 (폼 시트백, 폼 시트쿠션, 시트백 등)
시트 쿠션은 70개의 brick 요소로 메싱되어있습니다. 외에 물성은 다음과 같습니다.
- Quadratic bulk viscosity : 1.1
- Linear bulk viscosity : 0.05
- Hourglass viscosity coefficient : 0.1
더미와 시트 지지대는 Shell 요소로 모델링되었으며, 4871개의 4-node shell과 203개의 3-node shell입니다. (더미는 5004 shell개 시트 70개) 더미를 감싸는것을 정의하는데에 아주 작은 밀도의 물성이 사용되기 때문에 작은 Time Step을 피하기 위해 /DEL/SHELL/1 옵션이 활성화 되는 것이 좋습니다.
쉘 특성
- Belytschko hourglass formulation (Ishell 4)
- Membrane hourglass coefficient : 0.01 (디폴트)
- Out of plane hourlgass : 0.01 (디폴트)
- Rotation hourglass coefficient : 0.01 (디폴트)
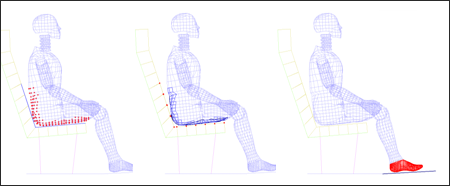
더미와 시트쿠션 사이의 컨택과 바닥과 발부분의 컨택은 Type 7번의 페널티 메소드가 적용된 인터페이스가 사용됩니다. 추가로 바디와 시트사이의 대칭 컨택이 적용되게 됩니다.
대칭적인 인터페이스 사이의 간격은 5mm로 동일하며 다른 인터페이스에서는 0.5mm로 설정됩니다.
Type 7 인터페이스는 면과 면 사이에 슬라이딩이 발생 할 수 있게 합니다. Coulomb friction이 적용 될 수 있으며 게다가 critical viscous damping coefficient는 슬라이딩에 대한 댐핑을 적용하기 위해 정의 될 수 있습니다.
대칭 인터페이스 특성 :
- Coulomb friction (Fric flag) = 0.3
- Critical damping coefficient (Visc flag) = 0.05
- Scale factor for stiffness (Stfac flag) = 1
- Sorting factor (Bumult flag) = 0.20
RADIOSS Option Used
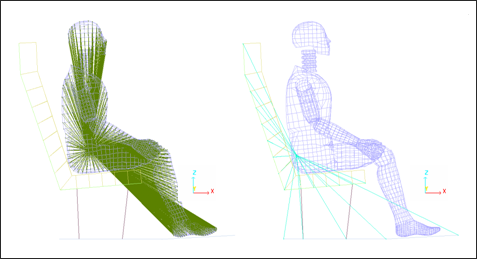
바디를 시트에 포지셔닝 시키는 목적은 정적 평형을 얻기 위해 준정적 접근을 이용하기 때문입니다. (다만 포지셔닝 상태는 본 예제에서는 포함하지 않습니다.) 이처럼 더미의 모든 절점들이 더미의 초기 상태를 유지하기 위해서 글로벌 강체(rigid body)에 위치해 있습니다.
CPU의 사용량을 절약하기 위해서 두번째 글로벌 강체에는 시트와 바닥부분이 포함되며 시트 쿠션 파트는 해석이 진행되는 동안 요소들이 활성화 되기 때문에 제외합니다.
ICoG가 1인 시트의 RBODY는 무게 중심은 마스터와 슬레이브 절점 좌표를 사용하여 계산하고 마스터 절점이 무게중심점으로 이동하게 됩니다. (정확하게는 질량과 관성이 위치하는 부분)
ICoG가 3으로 설정된 더미의 RBODY에서는 무게중심이 사용자가 설정한 마스터 절점 위치에 설정됩니다. 추가된 질량이나 관성은 마스터 절점 좌표로 이동하게 됩니다.
마스터 절점 좌표와 Skew는 오리지날 RBODY의 pelvis(골반) 파트로 부터 추출되게 됩니다.
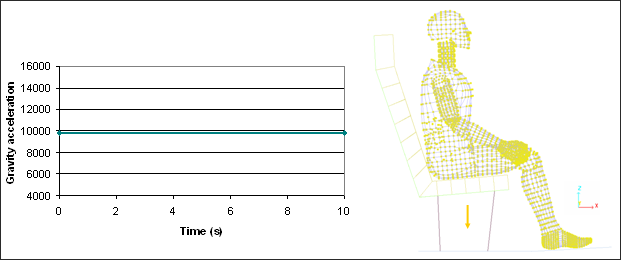
중력은 모델의 모든 절점에 적용됩니다. Z 방향의 중력 가속도는 시간에 따라 적용되게 되며 /GRAV 카드를 스타터 파일 (*_0000.rad)에 적용함에 따라 활성화 시킬 수 있습니다.
시트의 6개의 강체모드는 고정된 강체의 마스터 절점이 시트에 붙는 것이 완료되면서 제거됩니다. out of plane 진동을 제한하기 위해서 더미에 생성된 RBODY의 마스터 절점을 Y 병진 방향으로 고정합니다.
정적 해석 : 정적 평형을 위한 중력 하중의 준정적 대응
explicit 시간 적분 방법은 노드의 가속 계산과 함께 시작됩니다. 동적 하중 시뮬레이션에서는 이러한 방법이 효율적입니다. 하지만 동적 해석 기법을 경유하는 준정적 시뮬레이션은 정적 평형을 수렴하기 위해서 가능한 동적 하중의 영향을 최소화 시켜야만 합니다.
이는 일반적으로 동적 해석 이전에 프리로딩 케이스로 묘사되곤 합니다. 이처럼 중력 하중의 준 정적 해석은 시간에 따른 응답의 정적 파트입니다.
동적 영향을 줄이기 위해서 아래 3개의 옵션이 엔진 파일에서 사용되게 됩니다.
- Kinetic relaxation (/KEREL)
- Dynamic relaxation (/DYREL)
- Rayleigh damping (/DAMP)
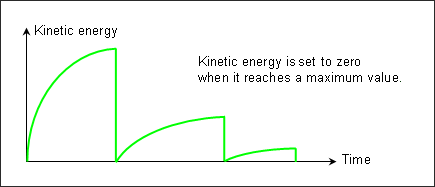
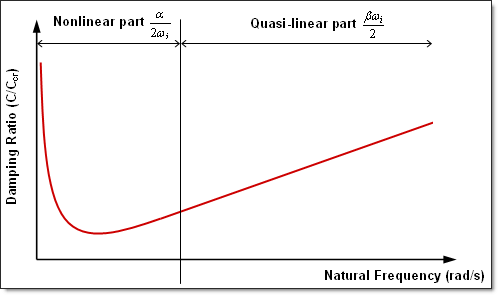
Kinetic Relaxation Method
운동 에너지가 최대로 달하는 경우 이 값을 0으로 변경시켜주며 이 옵션은 엔진 파일에 /KEREL을 사용하면 됩니다.
Dynamic Relaxation Method
동적 방정식에 부분적인 질량 매트릭스와 댐핑 매트릭스를 적용하면서 동적 하중이 댐핑되는 효과를 얻을 수 있습니다.
여기서 B는 relaxation value이며 (추천되는 디폴트 값은 1) T는 댐핑이 되는 간격을 의미합니다. 아래와 같이 viscous stress tensor가 stress tensor에 추가되게 됩니다.
Explicit 코드를 사용한 Dashpot 하중의 적용은 속도 방정식의 변형을 감소시켜주게 됩니다.
이 옵션은 엔진 파일에 /DYREL 키워드를 입력하는 것으로 적용 할 수 있습니다.
Rayleight Damping Method
위와 마찬가지로 동적 하중은 동적 방정식에 부분적인 질량과 댐핑 매트릭스를 적용하는 것으로 부터 댐핑 효과를 얻게 되는데 여기에 강성 매트릭스까지 더한 결과가 Rayleight Damping입니다.
이러한 단순화된 접근 방식은 직교 변환을 이용하여 N형 비결합 방정식의 글로벌 평형 방정식을 감소시킬 수 있습니다. 이 댐핑는 비례적인 비결합인 것으로 알려져 있습니다.
여기서 a와 B는 미리 정의된 상수들입니다. 비율적인 댐핑 가정을 사용한 직교 변환은 아래와 같은 식을 유도하게 됩니다.
S는 시스템의 댐핑 비율 그리고 W는 시스템의 고유 진동수를 의미합니다.
만약 사용자가 실험 결과를 갖고 있다면, 비율적인 값들인 a, B를 계산하는 것이 가능합니다. 이는 아래 식과 같이 두개의 변수를 갖고 있는 방정식을 푸는것으로 얻을 수 있습니다.
만약 여러개의 주파수들을 이용 가능하다면, 계산된 값들의 평균 a와 B가 사용 될 것입니다.
이런 비율적인 댐핑 모델은 복잡한 구조물에는 추천하지 않습니다.
해당 댐핑 옵션은 엔진 파일에 /DAMP 키워드를 입력하는 것으로 사용 가능합니다.
Paremeters Used
이번 예제에서 a와 B는 아래와 같은 값들을 사용하게 됩니다.
– First case : a = 10 B = 10
– Second case : a = 0 B = 10
– Third case : a = 10 B = 0
– Fourth case : a = 20 B = 0
결과 가정은 다음과 같습니다.
– First case : [C] = 10[M] + 10[K]
– Second case : [C] = 10[K]
– Third case : [C] 10[M]
– Fourth case : [C] = 20[M]
시뮬레이션 결과와 결론
커브와 애니메이션
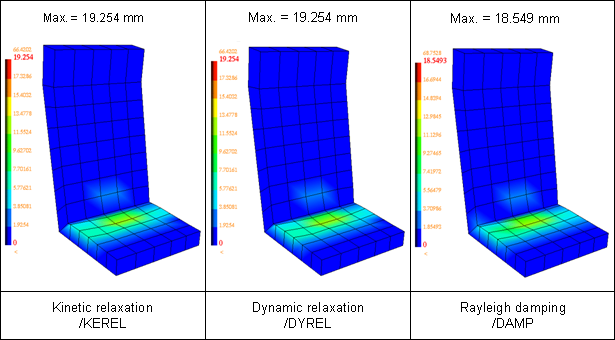
/KEREL 옵션이 적용된 Kinetic Relaxation 결과
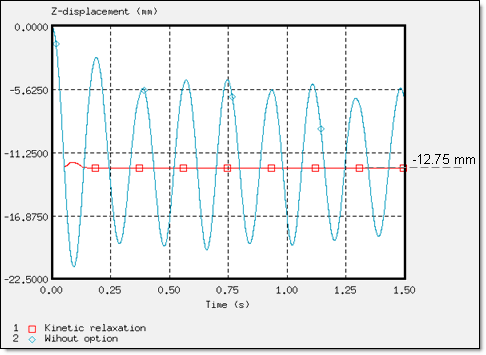
더미에 연결된 RBODY의 마스터 절점에서의 Z방향 변위
모델의 운동에너지
/DYREL 옵션이 적용된 Dynamic Relaxation 결과
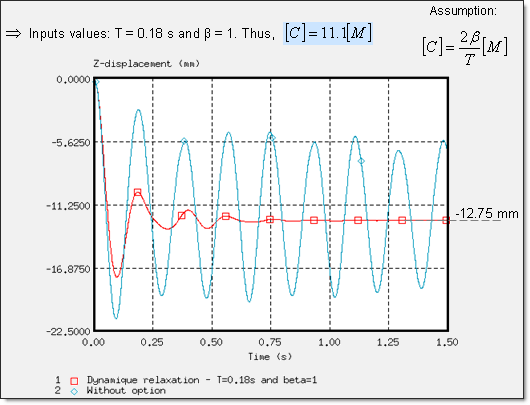
더미에 연결된 RBODY의 마스터 절점에서의 Z방향 변위
더미에 연결된 RBOYD의 마스터 절점의 Z방향 속도
/DAMP 옵션이 적용된 Rayleigh Damping 결과
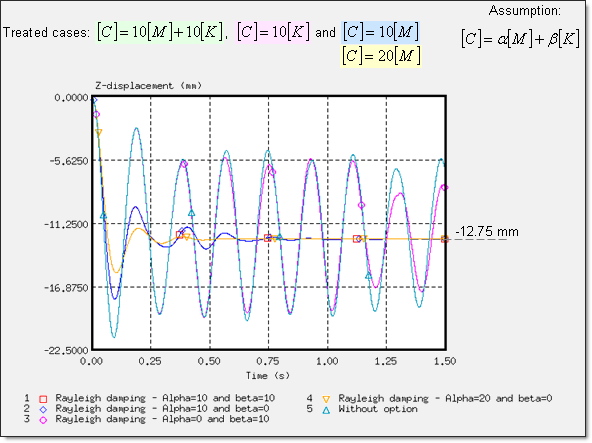
더미에 연결된 RBOYD의 마스터 절점에서의 Z방향 변위
더미에 연결된 RBOYD의 마스터 절점의 Z방향 속도
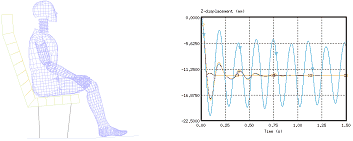
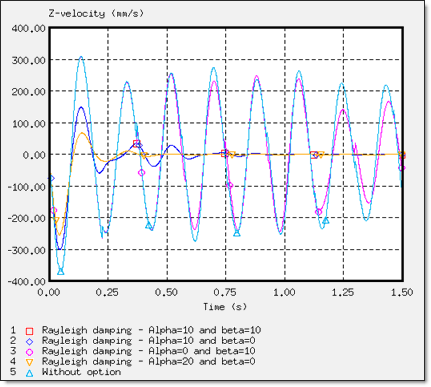
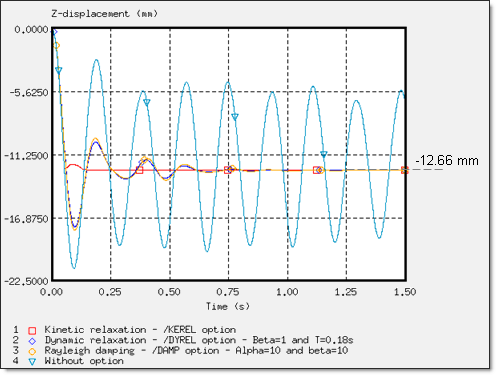
Comparison of the Different Approaches
시간 t = 1.48초 에서의 절점 변위 비교
3가지 접근 방식의 결과 비교
결론
정확한 결과를 보장하는 정적 평형 상태를 수렴하고자 댐핑 방법이 사용된건 부정 할 수 없습니다. 특히 매우 미세한 진동이 유발되는 시트와 같은 약한 강성을 지닌 모델 해석 문제에선 정적 평형을 유지시키기 위해 댐핑을 적용해야 합니다.
/KEREL이 적용되는 kinetic relaxation은 정적 해석에 대한 빠른 수렴 능력을 갖는 것이 상대적으로 효율적이라는 것을 보여주고 있습니다. 게다가 별도의 인풋을 필요로 하지 않기 때문에 사용하기 편리하다는 장점도 있습니다. (해석 결과의 안정성은 0.137초에서 부터 얻을 수 있습니다.)
/DYREL과 /DAMP 옵션은 viscous 댐핑을 기반하여 얻어집니다. 같은 반응에 대해 3번의 진동을 보여주며 안정성은 0.75초에서 얻을 수 있습니다. 더욱이 dynamic relaxation과 Rayleigh damping 방법은 시트 쿠션의 낮은 강성 때문에 (영률 값이 0.2MPa) 이번 문제에서는 기본적으로 동일한 값을 나타내고 있습니다. 단, Rayleight 가정에서는 질량과 무게 강성 사이의 균형이 깨지게 됩니다.
게다가 모델에 적용된 경계조건과 하중은 지배적인 고유주파수가 사용되는 것을 묘사한 문제를 유도하게됩니다. 이처럼 오직 하나의 파라미터 a는 동적 완화 가정으로 돌아가기 위한 물리적 거동을 묘사하기 위해 필요하게 됩니다.
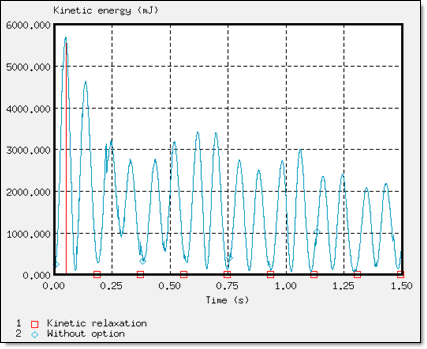
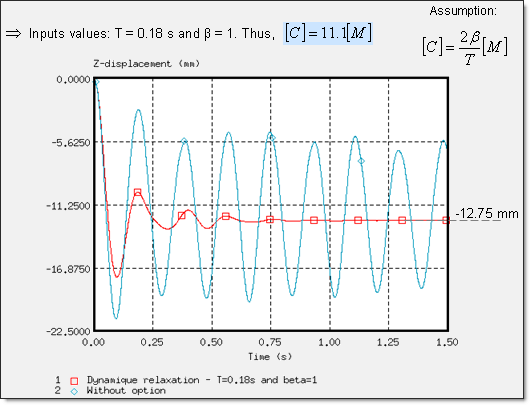
B = 1이고 T = 0.18을 사용한 dynamic relxation 그리고 B = 10인 Rayleight damping으로 사용자는 아래와 같은 값을 얻을 수 있습니다.
- Dynamic relaxation :
- Rayleight damping :
[C] =
[M] + 
[K] ≈ [M] ≈ 10[M]
결론을 내리자면 RADIOSS에서 단일 해석 수렴 후의 이러한 접근들을 하는것이 가능하며, 더미의 변위는 Z방향을 따라서 -12.66mm 그리고 시트 쿠션에도 동일한 변형이 발생 됨을 알 수 있습니다.
끝.
공략 17편 – 17 – Box Beam
|
<-- 이전 글 보기
|
다음 글 보기 –>
|