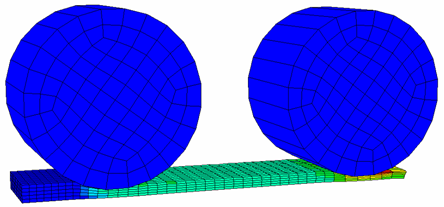
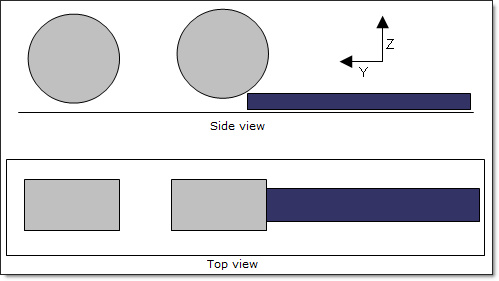
본 예제의 목적은 아래 그림과 같이 2개의 회전하는 실린더 밑에 깔린 메탈 스트립의 라미네이션을 RADIOSS로 구현해보는 것입니다. 크고 작은 변형률에 대한 가정들이 각각 적용됩니다. 메탈 스트립의 두께를 묘사하기 위한 요소 개수에 따른 해석 결과에 대한 영향과 요소 계산 방법을 논의 할 예정입니다.
물리적 문제 묘사
이번 해석은 레일 롤링을 시뮬레이션으로 구현합니다. 메탈 스트립의 두께를 감소시키기 위해서 두 개의 롤러가 메탈 스트립을 통과하게 되는데 이때 롤러에는 6.85 rad/s라는 일정한 각속도가 적용되며 메탈 스트립은 무빙 머신 배드를 따라서 드래그됩니다. 이러한 과정은 준정적 해석이 고려되야 하며 주로 압축으로 인한 변형이 상당히 발생 할 수 있습니다.
단위 : mm, s, Mg, N, MPa
롤러와 메탈 스트립 모두 순수 스틸로 구성되어있으며 이를 구현하기 위해 등방 탄소성 물성인 /MAT/LAW2를 사용합니다.
- Initial density: 7.8 x 109 Mg/mm3
- Young modulus: 210000 MPa
- Poisson ratio: 0.3
- Yield stress: 170 MPa
- Hardening parameter: 400 MPa
- Hardening exponent: 0.475
주의 : 본 예제에서는 마찰 열에 의한 열변형은 고려하지 않고 아래 조건에서 진행한다고 가정합니다.
- Temperature exponent: 1
- Melting temperature: 2073 K (around 1800°C)
- Specific heat at constant pressure Cp: 460 J/Kg.K
- Geometry: 메탈 스트립은 80 x 20mm의 크기이며 롤러는 100 mm 반경의 실린더입니다. 첫번째 롤러를 통과하면 스트립의 두께는 7mm로 감소하게되고, 그 다음 통과 후 5mm가 됩니다.
해석, 가정 그리고 모델링 묘사
모델링 기법
많은 요소들이 메탈 스트립을 따라서 이동하는 것이 필수적인건 아니지만 메탈 스트립의 두께 방향으로의 정확한 응력 분포를 알고자 한다면 최소 5겹의 요소가 존재해야합니다. (보고자 하는 결과에 따라서 때로는 5개의 층도 많은 것일 수 있습니다.) 이러한 요소에 대한 논의는 해석 전반부에서 다룰 예정입니다.
롤러의 요소들을 First order로 생성하는 것은 모델의 곡부를 완벽하게 만들어대는 것이 어려울 수 있습니다. 좋은 결과를 얻기 위해서는 가능한 요소를 세밀하게 생성하는 것이 중요합니다.
무빙 머신 베드는 모델링되지 않았으며, 메탈 스트립의 하단부를 Z 방향으로 구속하여 이를 구현합니다. 그리고 초기 속도는 메탈 스트립에 적용됩니다. 메탈 스트립과 롤러 사이에 발생되는 마찰력은 쿨럼 마찰로 구현하였고 0.3의 값이 적용됩니다.
롤러를 RBODY(강체)로 묶어서 강체로 설정하고, 이의 마스터 절점에 회전 속도를 적용합니다.
본 해석에서는 준정적해석으로 설정할 것이기 때문에 밀도를 인위적으로 10000배 증가시킵니다. 현재 사용된 밀도는 7.8e-05입니다. 그로 인해 타임스텝이 증가하여 해석 시간이 감소되고 운동에너지는 에너지 변형과 비교했을 때 무시할 만 합니다.
(밀도는 동적 영향이 무시될 만큼 증가 될 수 있습니다.)
RADIOSS Option Used
– 경계 조건 :
- 메탈 스트립의 하단부에 존재하는 절점들을 Z축 병진 방향으로 구속합니다. (무빙 머신 베드를 표현)
- 롤러의 마스터 절점은 X축 회전 방향을 제외하고 구속합니다.
– 강제 속도 :
- 2개의 롤러에 생성된 RBODY의 마스터 절점에 X방향의 각속도를 적용합니다.
– 초기 속도 :
- 메탈 스트립의 모든 절점에 X방향으로 500mm/s의 초기 속도가 적용됩니다.
– 컨택 인터페이스 :
- 메탈 스트립과 롤러간의 컨택을 구현하기 위해 인터페이스 타입7번이 사용됩니다. 마스터 면은 롤러의 외곽면으로 그리고 메탈스트립의 슬레이브 절점은 메탈 스트립의 /GRNOD/PART로 정의합니다.
- 롤러의 폭 방향으로는 1개의 요소만 존재합니다. 컨택의 최소 갭은 1mm로 지정됩니다.
시뮬레이션 결과
두께방향으로 요소 개수 차이에 따른 결과
본 예제 초반에 두께방향으로 5개의 요소를 지정해야한다고 언급했었는데 어떤 차이가 있는지 알아보도록 합니다. 층을 묘사하기 위한 요소 개수는 해석을 통해서 확인하고자 하는 결과에 따라 다릅니다. 만약 두께 방향의 응력 분포를 알아보고자 한다면 더 많은 요소 개수가 필요하게 됩니다.
요소 개수를 많게하면 좋은 결과를 얻게되지만, 해석 시간이 오래걸린다는 단점이 있습니다. 사용자는 이 둘 사이에서 적절하게 타협해야 합니다.
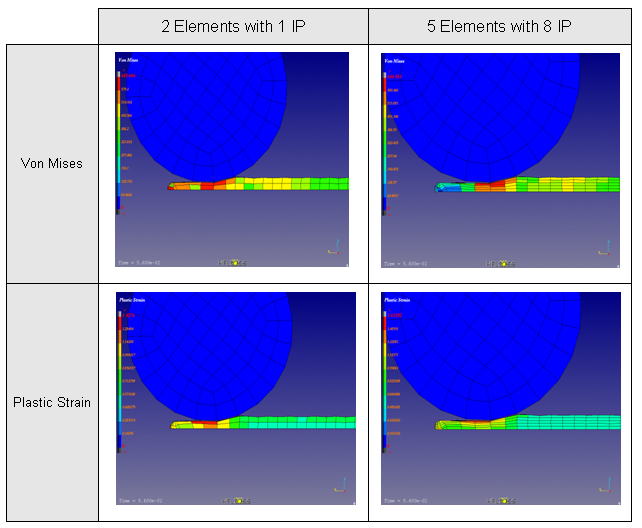
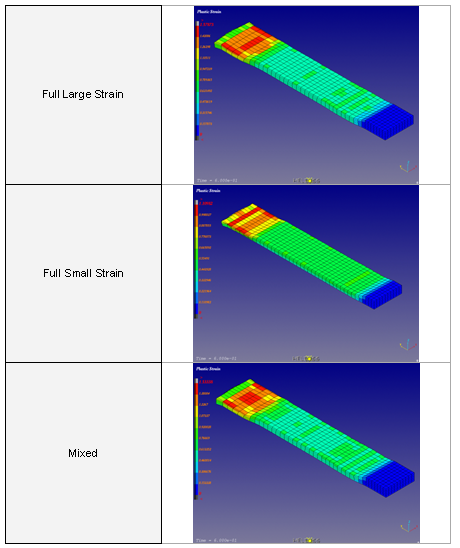
이에 더해 본미세스 응력과 소성 변형을 적분점의 개수를 다르게 하여 해석한 결과를 아래 그림으로 나타내고 있습니다.
두께를 2개의 요소로 묘사한 것은 응력 또는 변형률의 분포를 제대로 확인하기에 충분하지 않습니다. 최소 5개정도는 되야 적절합니다. 만약 변형된 형상이 자연스럽거나 층으로 구분되지 않는다면 요소를 조밀하게 생성하는 것을 고려하시기 바랍니다.
하지만 해석시간이 다소 증가한다는 것을 유의하셔야 합니다. 추가적으로 본 모델의 경우 2개보다 5개의 층으로 만든 모델이 12배만큼 더 해석시간을 필요로합니다.
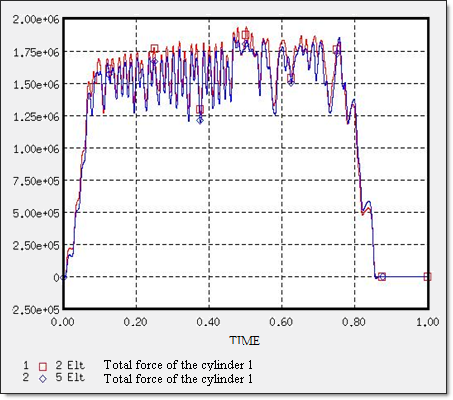
그렇다면, 응력 분포와는 다르게 반력의 경우는 어떨까요?
위 그림은 첫 실린더에서 발생한 반력입니다. 2개짜리 모델과 5개짜리 모델 둘은 거의 유사한 결과를 보여주게됩니다.그래서 언급했듯이 보고자 하는 결과에 따라서 요소 개수를 적절하게 사용해야 합니다.
Small Strain 계산 방식의 영향
일반적으로 대변형 문제를 해결 할 때, Large strain 계산 방식이 사용됩니다. RADIOSS에서는 이를 기본 설정으로 사용하고 있습니다. 하지만 small strain 계산 방식을 이용하는 것도 가능합니다. 이 방식은 대변형 해석에서는 매우 정확하진 않습니다. 하지만 해석 결과가 안정적이며 타입스텝이 급격하게 줄지 않는 장점이 있습니다.
실로, 대변형/회전 문제는 요소의 왜곡을 유발하고 이는 타임스텝이 상당히 작아지는 문제로까지 이어지게 됩니다. 그래서 네거티브 볼륨에러와 함께 해석이 중단되기도 합니다.
small strain 계산 방식은 t=0에서 Ismstr를 1로 설정하는 것으로 적용하는 것이 가능합니다. 또한 /DT/BRICK/CST를 이용하여 엔진카드에 크리티컬 타임스텝과 같이 입력하면 해석 도중에 네거티브 볼륨을 피하기 위해 large strain을 small strain 계산 방식으로 변경 할 수 있습니다.
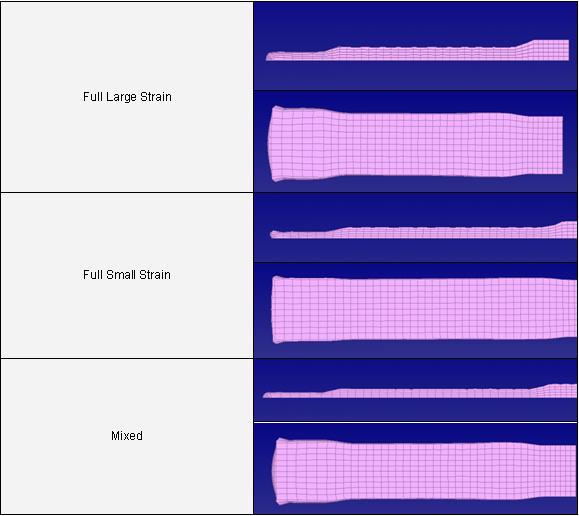
아래 그림은 이들의 결과와 둘을 혼합한 결과를 비교하도록 하고 있습니다. Large의 경우 small 대비 평균 타임스텝이 20%정도 크며 혼합형에 비해 3.5% 큽니다. 따라서 small strain 계산식을 사용하는 것이 해석 시간을 단축하기 위한 중요한 포인트입니다. 아래 그림을 보시면 변형 결과도 꽤나 만족 할 만 합니다.
하지만, 소성변형에 대한 결과를 확인했을 땐 다음과 같은 문제점들이 있습니다. 먼저 변형률 분포가 적절하지 않아보이는데 이는 매우 중요한 포인트입니다. 다음으로 최대 값에 차이가 있습니다. 이는 영구적인 변형이 보다 작게 표현되는 문제를 발생하게 됩니다.
이러한 케이스에서 몇몇 크리티컬 타임스텝에 도달하는 요소들에만 small strain 방식을 사용하는 것이 흥미로울수는 있습니다. 가령 요소 변형으로 인한 타임스텝 에러를 방지하기 위한 용도로 말입니다. 하지만 정확한 결과를 얻기 위해서는 small strain 방법이 체크되야 하며 이들의 수가 적은것이 좋습니다.
HA8 계산 방식
보다 개선된 solid 계산 방식은 HA8을 이용하면 일반적인 8개의 적분점으로 계산하는 방식의 문제점들을 극복 할 수 있습니다. (기존 Isolid 12, 14, 개선 Isolid 24).
예를 들어 순수굽힘의 케이스에서 shear-locking이 보다 단단하게 나오던 문제점을 개선합니다. 또한 small strain 계산 방식을 적용하는 것이 가능합니다. (기존 8적분 방식은 불가)
또한 각 방향에 대해 적분점의 개수를 9개까지 증가시키는 것도 가능합니다.
Icpre 플래그에 따라서 HA8 계산 방식은 reduced pressure integration을 사용 할 수 있습니다. 본 예제에서 이러한 플래그를 통해 적절한 값을 찾을 수 있습니다.
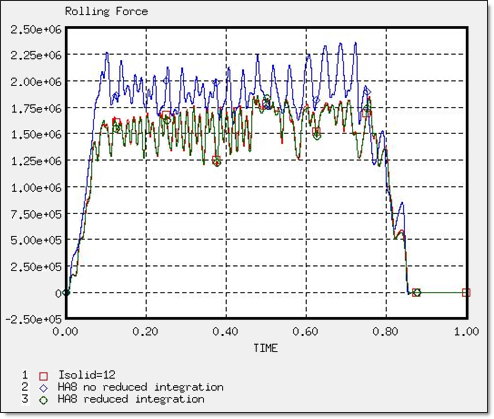
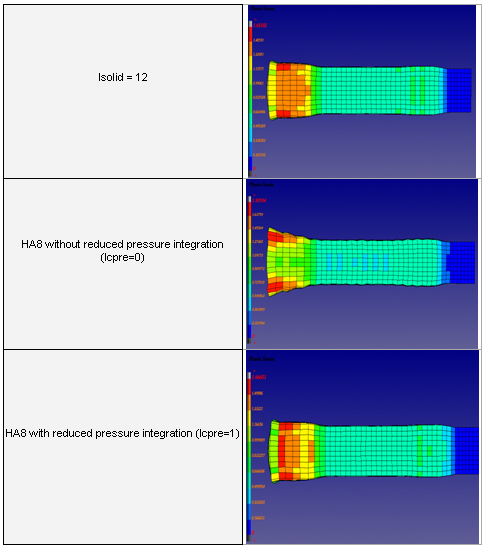
아래 표는 Isolid 12와 reduced integration이 적용되고 안된 HA8 모델을 비교하고 있습니다. 표에도 보이듯이 reduced integration의 적용 여부에 따라 결과가 다른 것을 볼 수 있으며 적용 된 결과가 보다 좋은 값을 나타내는 것을 볼 수 있습니다.
따라서 HA8 계산 방식을 사용 할 때는 항상 reduced pressure integration을 적용해야 합니다. 단 8-node thick shell 계산식을 적용 할 때는 반드시 reduced pressure integration 옵션을 해제해야 합니다.
온도의 영향
이러한 제품 성형과 같은 과정에서 엔지니어는 실린더의 변형을 막기 위해 실린더에 작용하는 영향들을 최소화 시킬 방법을 강구해야 합니다. 제품 성형에서 이러한 영향을 최소화하는 방법으로 대표적인 것은 높은 온도입니다. RADIOSS에서는 이러한 온도의 영향을 적용하는 것이 가능합니다.
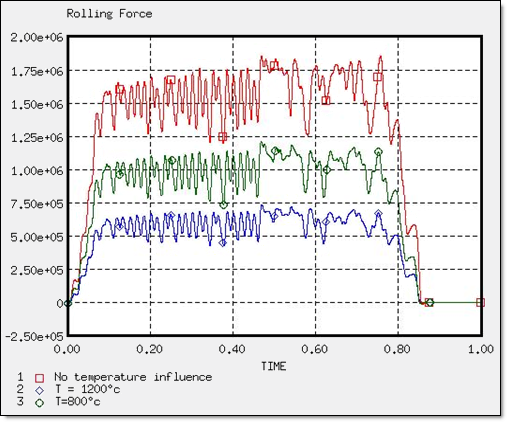
다음 표는 온도에 따른 롤링 하중을 보여주고 있습니다. 높은 온도일 수록 낮은 저항을 나타내고 이는 또한 메탈 성형에서 사용자가 고민해야 하는 포인트입니다.
결론
메탈 스트립을 2개의 롤 실린더를 이용하여 압축시키는 것을 RADIOSS로 진행해봤습니다. 이에 대해서 정확한 결과를 얻기 위한 두께 방향으로 충분한 요소개수가 얼마인지를 알아봤습니다. 또한 small strain 방법을 적용하면 결과는 좋지 않지만 해석 시간이 짧아지는 장점을 확인했고 적분점의 개수에 따른 해석 결과의 영향 그리고 온도에 대한 영향까지 확인했습니다.
끝.
RADIOSS 공략 25편 – Spring back
|
<-- 이전 글 보기
|
다음 글 보기 –>
|