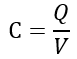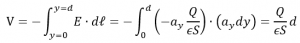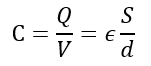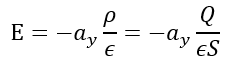Flux로 풀어보는 전자기학 1편 – Capacitor

Keyword: Capacitor, Capacitance, Electric field, Electric flux density

목적:

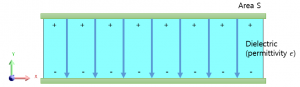
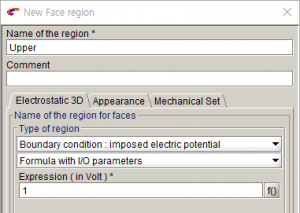
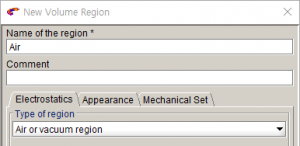
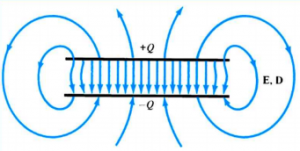
이번 예제는 간단한 Capacitor 구조에 대한 E (Electric field)와 D (Electric flux density) 그리고 C (Capacitance) 값을 Flux로 계산하고, 기본이론과 비교합니다. 모델은 아래의 그림과 같은 구조를 가지고있으며 Flux에서는 3D 모델로 구성합니다. Capacitor는 공기로 채워져 있고, 인가되는 전압은 상단 1V, 하단 0V이고 평판의 면적은 1, 거리는 0.3m 입니다.

Flux 모델구성:

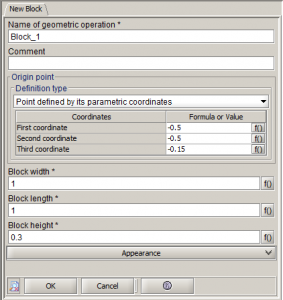
1. 박스생성
   1. Construction >> Block >> New
   2. (-0.5, -0.5, -0.15), width: 1, length: 1, height: 0.3
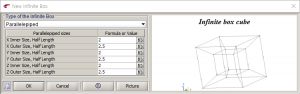
2. Infinite Box생성
   1. Geometry >> Infinite box >> New
   2. Parallelepiped, Inner: 2, Outer: 2.5
   3. Geometry >> Infinite box >> Complete Infinite box
3. 면 전압 설정:
   1. Physics >> Face region >> New
   2. Boundary condition : imposed electric potential로 전압 인가 (Volt)
4. 유전체 및 진공 상태 설정: Volume region
   1. Physics >> Volume region >> New
   2. 각 타입 지정 (Infinite box: Air or vacuum, 유전체: Dielectric region)

기본 이론치:

두 평판 사이에 직류 전압이 인가되면 전하의 전이가 발생되어 각 +Q, -Q의 전하를 축적하게 되고, 두 평판은 아래와 같은 전기장을 발생시킵니다.

축적된 전하량 Q는 아래의 식으로 나타내어 지고,

여기서 비례상수 C는 정전용량(Capacitance)이라고 부르며 도체에서 단위전위만큼 올리기 위해 추가로 필요한 전하의 양으로, 이 값은 축전기(Capacitor)가 전하를 저장할 수 있는 능력을 나타냅니다.

위 식을 C에대해 다시 나타내면

가 되고, V는 아래의 식으로 나타내어 집니다.

따라서, 정전용량은 아래의 식으로 나타낼 수 있습니다.

또한, 생성되는 E (Electric field)와 D (Electric flux density)는 아래의 식으로 표현 됩니다.

각 수식에 값을 대입하여 보면

∵ 는 Y 방향 벡터로 평판 끝에서 발생하는 가장자리 전기장을 무시하여 -1로 계산

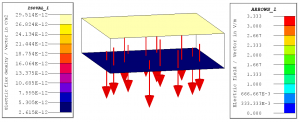
Flux 시뮬레이션 결과:

위에 나온 D 값에 평판의 면적을 곱하면 Q 값을 얻을 수 있고, 이 Q 값과 인가된 전압을 이용하여 정전용량을 구하면

이론과 시뮬레이션 결과를 비교하여 보면, 두 값이 거의 유사함을 알 수 있습니다.