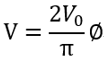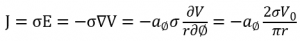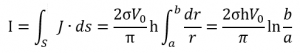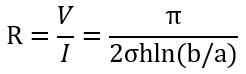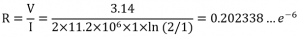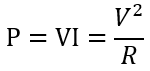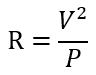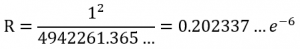Keyword: Resistance, Conductivity, Conductor

목적:

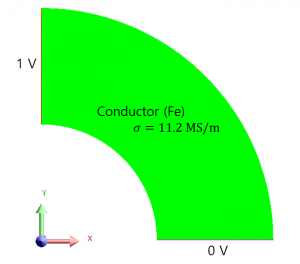
이번 예제는 σ의 전도도를 가지는 도체 매질에 대한 저항(Resistance)을 구하고, 기본이론과 비교합니다. 모델은 아래의 그림과 같이 평평한 원형 워셔의 1/4 모양을 하고 있으며, 도체 매질은 철(Fe) 입니다. 인가되는 전압은 상단 1V, 하단 0V이고 평판의 면적은 1, 안쪽 반지름은 1m, 바깥쪽 반지름은 2m 입니다.

21

22

Flux 모델구성:

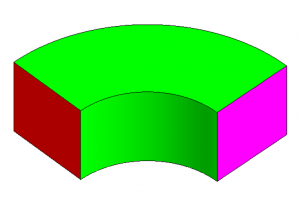
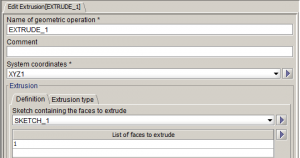
  1. 워셔생성
    1. Tools >> Sketch >> New
    2. Construction >> Rectangle >> Rectangle diagonal
    3. Construction >> Line >> Polyline
      23
    4. Tools >> Extrusion >> New
    5. Definition: SKETCH1, 1, Extrusion Type: Around axis, 5, 902425
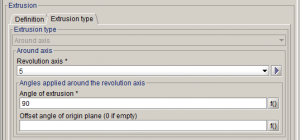
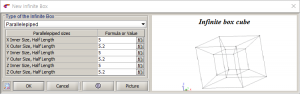
  2. Infinite Box생성
    1. Geometry >> Infinite box >> New
    2. Parallelepiped, Inner: 5, Outer: 5.2
      26
    3. Geometry >> Infinite box >> Complete Infinite box
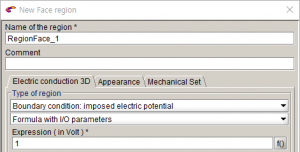
  3. 면 전압 설정:
    1. Physics >> Face region >> New
    2. Boundary condition : imposed electric potential로 전압 인가 (Volt)
      27
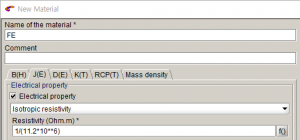
  4. 재료 물성 설정
    1. Physics >> Material >> New
    2. J(E) : 1/(11.2×캡처)28
  5. 도체 및 진공 상태 설정: Volume region
    1. Physics >> Volume region >> New
    2. 각 타입 지정 (Infinite box: Inactive region, 도체: Conducting region)

기본 이론치:

도체 양단에 전위차를 발생 시키면 도체를 따라 전하가 이동하며 전류가 생성되고, 도체에는 전류의 흐름을 방해하는 저항이 형성됩니다.

임의의 형상을 갖는 도체의 경우 도체 내부에 흐르는 총 전류를 구하여 전압과 전류의 비로 저항을 계산해 낼 수 있습니다.

총 전류를 구하기 위해서는 전류밀도를 먼저 계산하여야 하며, 전류 밀도는

29

도체의 각 위치에 따른 전압의 크기를 식으로 나타내면,

210

따라서, 전류밀도는

211

총 전류는 전류밀도를 적분하여 구할 수 있으며,

212

저항은 전압과 전류의 비에 의해 구할 수 있습니다.

213

위 식의 변수에 값을 대입하여 계산하면,

214

 

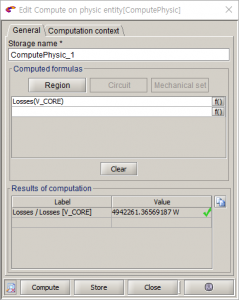
Flux 시뮬레이션 결과:

앞서 언급했듯이 도체에 전류가 흐르면 저항이 형성되고, 이 저항에 의해 전력의 손실이 일어납니다.

손실은 열과 빛과 같은 형태로 나타내어지며, Flux에서는 이 손실을 계산해 도체의 저항을 역으로 구하는 방법을 사용하도록 하겠습니다.

215

인가되는 전압을 알고있으므로 전류를 전압과 저항의 비로 나타내어,

216

저항을 좌변으로 옮기면,

217

218

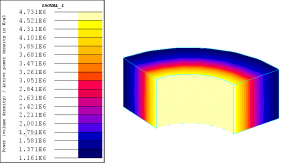
Flux에서 계산된 결과를 확인하여 보면, 워셔 안쪽 면적에 손실이 더 많이 일어나는 것을 확인할 수 있는데, 그 이유는 바깥쪽에 비해 안쪽의 면적이 작기 때문에 전류의 흐름이 세져 나타나는 현상입니다.

총 손실은 각 손실 값의 적분을 통해 구해지고,

219

계산된 값을 식에 대입하면,

220

이론과 시뮬레이션 결과를 비교하여 보면, 두 값이 거의 유사함을 알 수 있습니다.

<-- 이전 글 보기

다음 글 보기 –>