힘을 가해 연필이 두 동강 나는 경우에는 어떤 해석을 해야할까요? 정답은 본문에서 확인하세요!
Linear? Nonlinear?
1. 선형(Linear)
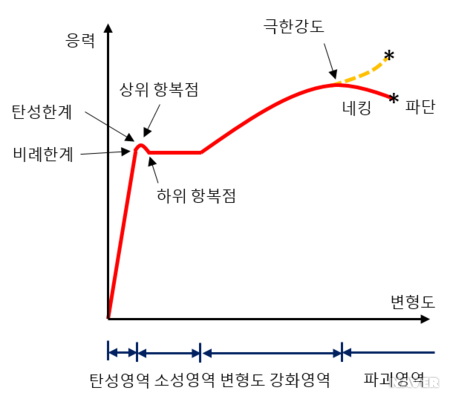
선형(Linear)은 직선을 의미하며, 일반적인 재료의 stress-stain(응력-변형률 곡선) 그래프에서 Linear 구간은 재료의 탄성 영역을 의미합니다. 즉, 선형해석(Linear analysis)은 재료의 탄성 영역 내에서 하는 해석이라고 할 수 있습니다.
사진: 응력-변형률 곡선 (출처 : 한국물리학회)
원래 항복점(yeild point)까지는 변형력과 변형이 비례하고 힘이 없어지면 원래 상태로 돌아가지만(=탄성;elasticity), 항복점을 넘어서면 영구적으로 모양이 바뀌고(=소성;plasticity) 외력이 너무 강하면 파열합니다.
현실에서는 항복점을 지나면 재료는 비선형 거동을 하지만, 이론적으로 선형 가정 상태에서는 외부 하중에 의해 재료가 항복점을 지나도 계속 선형이었던 직선을 따라서 해석을 수행하기 때문에 선형해석에서는 파열의 모습을 보여주지 않습니다.
그래서 위의 사진처럼 연필이 부러지는 등의 영구 변형이 발생하는 경우를 확인하기 위해서는 선형해석이 아닌 비선형해석을 해야합니다.
이러한 선형 해석을 활용하는 경우는 계산의 편의와 조건 변화가 미비한 경우에 가정해서 사용하는 것으로, 해석자는 구조물이 힘을 받을 때 어느 지점까지가 형상의 안전 범위인지 또는 파손 범위인지를 Maximum Stress와 Yield 또는 Ultimate Stess 사이를 비교하여 결정할 수 있어야 합니다.
여기서 선형 정적 해석(Linear static analysis)까지 말씀드리자면, 정적(Static)은 시간에 따라 Force가 변하지 않는 것을 말하기 때문에 선형 정적 해석은 재료의 탄성 영역에서, 시간이나 변위에 종속적이지 않는 해석이라고 할 수 있습니다. 선형 정적 해석은 대부분 일반적으로 항공우주, 자동차, 해양구조물, 도시 공학 등 다양한 산업군에서 많이 활용하고 있습니다.
2. 비선형(Nonlinear)
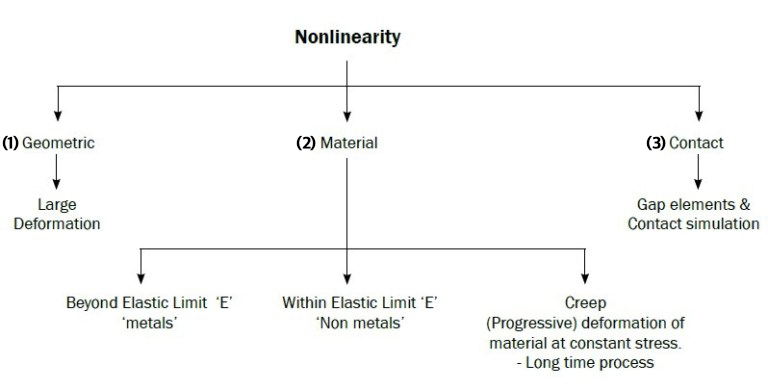
선형해석이 탄성 영역에서의 해석이라면, 비선형해석(Nonlinear analysis)은 탄성 영역을 벗어난 경우 적용하는 해석입니다.
비선형해석은 다음과 같은 상황에서 적용합니다.
1) 기하학적으로 해석 모델이 크게 변할 때 : 해석 모델의 변형이 보통 모델의 전체 크기의 5%를 벗어날 때 적용합니다.
2) 재료의 소성 영역을 고려할 때 : 선형 정적 해석과 달리 재료의 탄성영역 뿐 아니라 소성 영역까지 고려할 때 적용합니다.
3) Contact를 고려해야 할 때 : 두 부품이 외부 하중에 의해 접촉되는 것을 고려하기 위해 적용합니다.
감사합니다.
한국알테어
