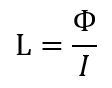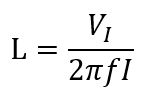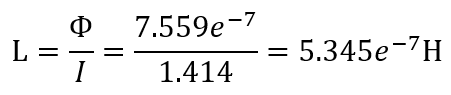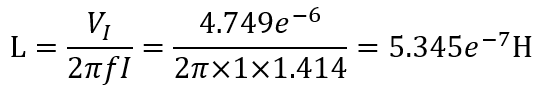Keyword: Inductance, Inductor

목적:

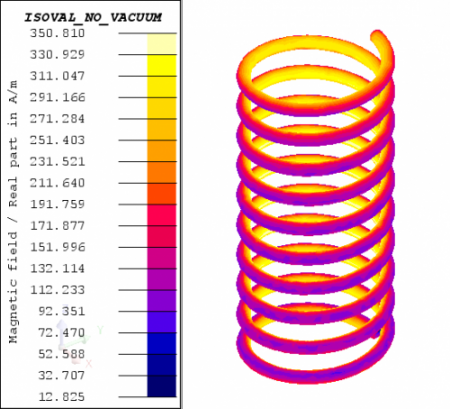
이번 예제는 솔레노이드 코일에 전류가 흐르고 있을 때 코일이 가지는 인덕턴스를 구하고, 기본이론과 비교합니다. 모델은 아래의 그림과 같이 반지름 1mm의 원형 단면을 가지고 있으며, 길이는 50mm, 감은 수는 10회, 도체 매질은 구리(Cu), 인가되는 전류는 1A(rms) 입니다.

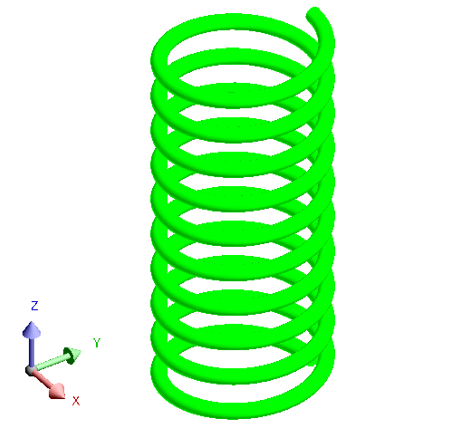41Flux 모델구성:

  1. 솔레노이드 코일 생성
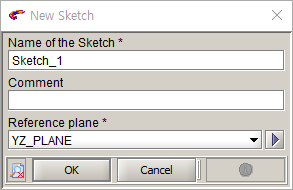
    1. Tools >> Sketch >> New : YZ_Plane42
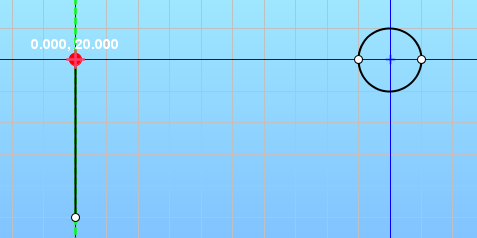
    2. Construction >> Circle >> Circle center + radius
    3. Center: (10, 20), Radius: 1
    4. Construction >> Line >> Polyline
    5. Point 1: (0, 20), Point 2: (0, 15)43
    6. Project >> Close Sketch context
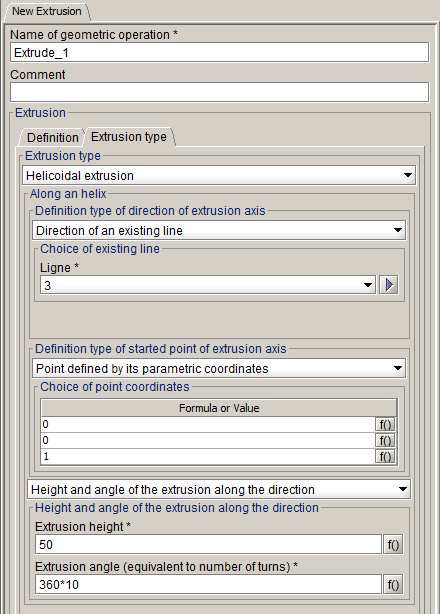
    7. Tools >> Extrusion >> New
    8. Definition: SKETCH_1, 1, Extrusion type: Helicoidal extrusion44
  2. Infinite Box생성
    1. Geometry >> Infinite box >> New
    2. Parallelepiped, Inner X,Y: 30, Outer X,Y: 35, Inner Z: 50, Outer Z: 5545
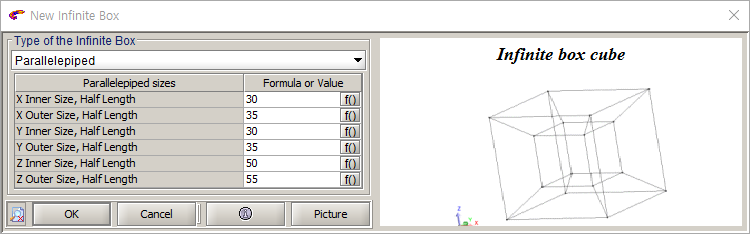
    3. Geometry >> Infinite box >> Complete Infinite box
  3. Mesh생성
    1. Mesh >> Mesh domain
  4. Circuit설정
    1. Physics >> Circuit >> Circuit editor context
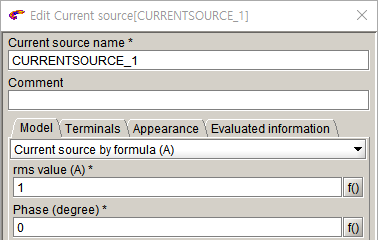
    2. Circuit >> Current source >> New로 인가 전류 설정46
    3. Circuit >> Stranded coil conductor >> New로 저항 설정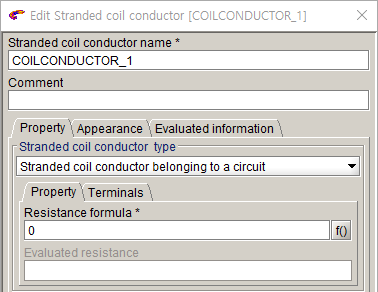47∵저항은 입력하는 물성치의 값으로 계산48
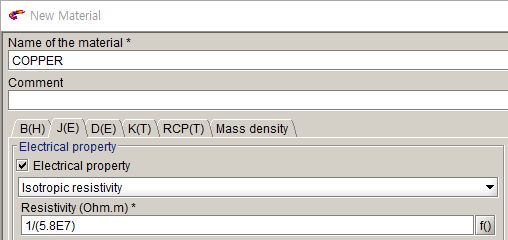
  1. 재료 물성 설정
    1. Physics >> Material >> New
    2. B(H): 1, J(E): 1/(5.8E7)49
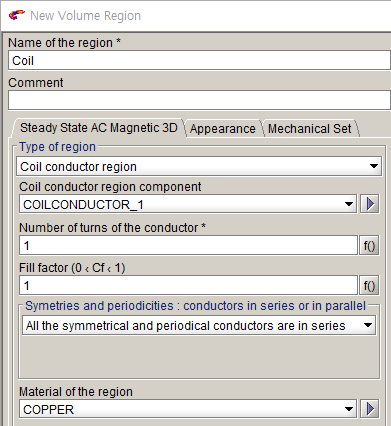
  2. 도체 및 진공 상태 설정: Volume region
    1. Physics >> Volume region >> New
    2. 각 타입 지정 (Infinite box: Air or vacuum, 도체: Coil conductor region)410

기본 이론치:

전류가 흐르는 도체 주변에는 자기장이 형성됩니다.

도체에 흐르는 전류가 교류인 경우 자기장의 세기는 전류에 따라 변화하고, 전류의 흐름을 방해하는 방향으로 도체 상에 전압을 발생 시킵니다.

이를 자기-인덕턴스라 부르고, 자기-인덕턴스를 갖는 것을 인덕터라 부릅니다.

도체의 인덕턴스는 다음과 같은 식으로 나타낼 수 있습니다.

411

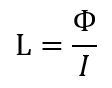
주파수가 높아질수록 인덕턴스 효과가 중요해지며, 주파수에 따른 식으로 나타내면

412

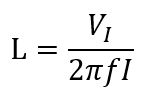
Flux 시뮬레이션 결과:

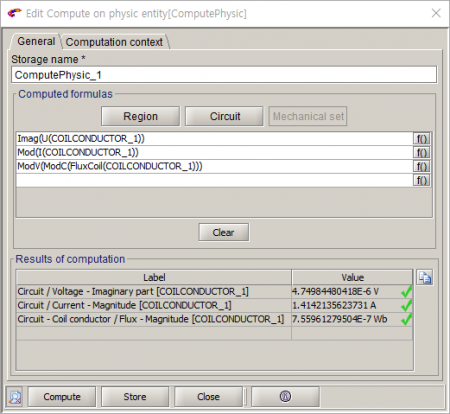
Flux에서는 해석 완료 후 도체에 걸리는 전압과 전류 그리고 자속을 측정하여 위의 이론 식에 적용하여 인덕턴스를 구하게 됩니다.

413

Flux의 computation 기능을 이용하여 도체에 걸리는 전압과 전류 그리고 자속을 구할 수 있습니다.

414

위에서 구해진 전압과 전류, 자속을 인덕턴스를 구하는 각 식에 입력하면,

415

416

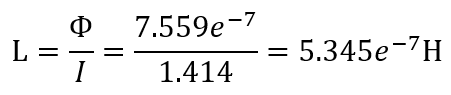
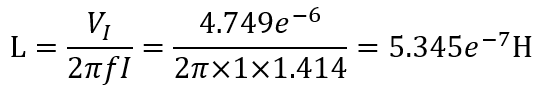
로 두 식이 같은 해를 가지는 것을 확인할 수 있습니다.


이전글