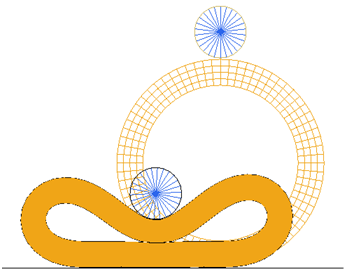
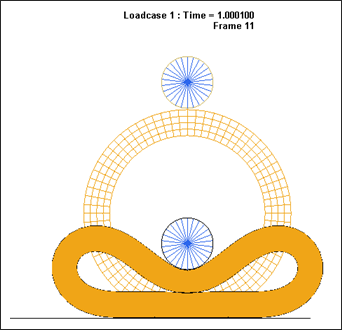
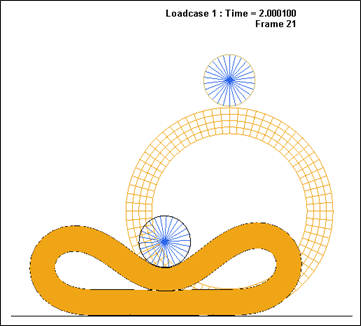
이번 예제에서는 평평한 강체 면에 놓여있는 고무링의 변형을 시뮬레이션으로 구현합니다. 놓여있는 고무링 위에 강체로된 롤러로 눌러서 고무링의 변형을 발생시킵니다. 변형이 발생하는 고무링 자체에 셀프 컨택을 적용하여 자체적인 관통 현상이 나타나지 않도록 설정합니다.
강체 롤러에 적용되는 하중은 2가지 스탭으로 나눠지는데, 먼저 롤러로 인해 고무링에서 셀프 컨택이 발생 할 수 있는 정도로 눌러줍니다. 그 다음 고무링은 평평한 강체 면을 따라서 점차적으로 이동하면서 회전하게 됩니다. 이때 고무링이 회전하기 때문에 컨택 면이 계속해서 변하게 됩니다.
본 해석은 RADIOSS의 Implicit 솔버를 이용하여 비선형 해석을 진행하며 이번 예제의 주된 목적은 RADIOSS impicit 솔버를 이용하여 탄소성 물성과 컨택이 포함된 고무링의 비선형적인 변위를 확인하는 것입니다.
물리적 문제 정의
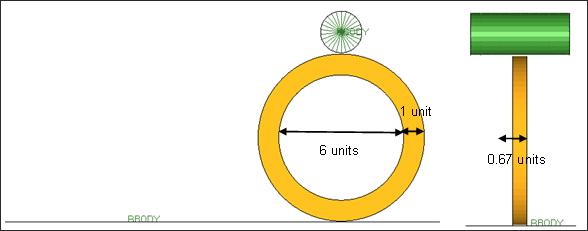
변형되는 고무링은 내경 6, 외경 8이며 두께는 0.67의 크기를 갖고 있습니다. 강체 롤러의 지름은 2이고 롤러와 바닥면의 두께는 0.1입니다.
본 예제의 모델을 확인하면 절반의 대칭 모델로 구성해도 되는데 풀 모델을 사용한 이유에 대해 의문을 품을 수 있을텐데 사실 처음에 고무링의 유발하는 과정에서는 절반의 모델로 대칭을 설정하여 해석해도 가능하지만, 두번째 스탭에서 고무링이 이동하는 과정을 구현하려면 전체 모델이 필요하게 되어 전체 모델을 이용합니다.
탄소성 고무링은 Ogden 물성을 이용하며, RADIOSS에서는 Mooney-Rivlin 물성인 /MAT/LAW42를 적용합니다.
자세한 값은 다음과 같습니다.
- μ1: 0.7
- μ2: -0.5
- α1: 2.0
- α2: -2.0
- Poisson’s ratio: 0.495
롤러와 바닥 면과 같은 강체들은 탄성 물성을 이용합니다. 하지만 1D 강체 링크는 각 배리어들의 절점에 포함되어 있기 때문에 이를 반드시 강체로 설정해줘야 합니다.
따라서 강체 배리어에 대한 물성을 다음과 같이 적용합니다.
- Density: 7.9e-9
- Young’s modulus: 600 MPa
- Poisson’s ratio: 0.3
해석, 가정 그리고 모델링 정의
Geometry 선형 (NLSTAT)와 Geometry 비선형 해석
Geometry 선형 해석은 모든 변형이나 움직임이 매우 작을 때 가능합니다. 구체적으로 모델 전체 크기에 대비하여 변위가 5% 이내인 경우입니다. 예를들어 고무링의 경우에 마지막 변형과 변형률이 5%보다 크기 때문에 NLSTAST을 사용하지 않고 대변형을 위한 NLGEOM 해석을 사용하게 됩니다.
모델링 방법
1) 메쉬와 특성
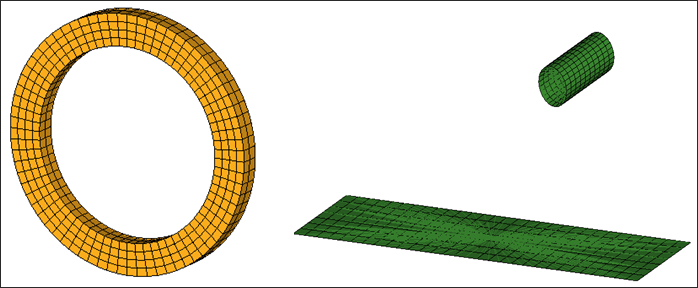
고무링 메쉬는 일반적인 Solid 요소를 사용하여 만들어졌으며 0.25의 크기를 갖는 4개 층의 요소들로 구성되어있습니다. 두께 방향으로는 0.335를 갖는 헥사 요소가 2개 층으로 이루어져있습니다. 바닥 면과 강체 롤러는 각각 0.01mm의 두께를 갖고 있으며, 면의 넓이는 0.75 * 0.467입니다.
고무링은 first order에 완전 적분 계산 방법이 적용됩니다.
RADIOSS에서 Solid에 대한 완전 적분을 적용하려면 Property에서 ISOLID 14를 사용하시면 됩니다.
/PROP/SOLID/5
WHEEL
14 10 1 222
바닥면과 롤러는 first order에서 감소적분이 적용된 shell을 사용하는데 이는 두께에 따라서 3개의 적분점이 사용됩니다.
해당 부분들은 주요 관심사가 아니기 때문에 완전 적분 계산 방식을 적용 할 필요가 없습니다.
/PROP/SHELL/6
BARRIER
1 2
3
0.01
2) 하중 및 경계조건
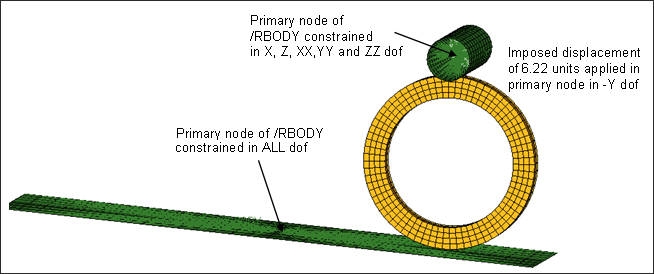
위에 언급했던 첫번째 스탭에 대한 하중은 아래 그림과 같이 적용됩니다.
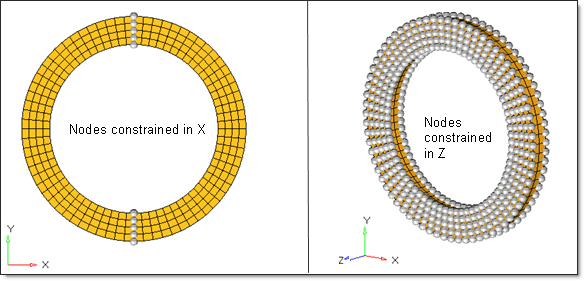
첫 스탭에 대한 경계 조건도 아래 그림과 같이 바닥면과 롤러에 적용됩니다.
바닥면은 모든 자유도를 구속했으며, 롤러의 경우 고무링의 셀프 컨택이 적용될 때 까지만 움직이기 위해서 Y방향으로의 6.22의 강제 변위가 발생하게끔 설정했습니다.
두번째 스탭에서 롤러는 계속해서 움직이고 회전하게되는데 이 방향은 X축을 따르고 있습니다. 그래서 X방향과 ZZ축으로의 회전이 적용되야 하며 이때는 스탭1에서 적용된 구속의 작동 멈춰야 합니다.
다시 설명하자면 고무링의 상부와 하부의 중간 절점들은 X방향으로 구속되어있던 경계 조건을 고무링이 움직일 수 있도록 풀어줘야 합니다. 이들 조건들은 /RBODY에 적용되어 있어서 2번째 스탭 전에 이들을 엔진 키워드를 통해서 구속을 멈추게 설정되었습니다.
/BCSR/TRA/X/
5 6 8 9 15 16 17 18
87 88 89 93 94 95 241 242
243 244 245 246 5717 5699 5681 5663
5662 5537 5517 5497 5477 5476 2269
/BCSR/ROT/Z
2269
3) 접촉조건 정의
다음과 같은 3가지 컨택을 정의해야 합니다.
- 롤러와 고무링 사이의 컨택
- 바닥면과 고무링 사이의 컨택
- 고무링 자체적인 관통을 방지하기 위한 셀프 컨택
롤러와 고무링 사이 그리고 고무링과 바닥 면 사이의 물리적 컨택 간격은 0.05로 설정했습니다. 컨택에 대한 최소 간격은 컨택의 영향으로 점차적으로 증가하게 됩니다.
컨택에 대한 마찰은 쿨럼 마찰을 이용했으며 이 값은 0.5가 모든 컨택에 대해 적용됩니다.
/INTER/TYPE7/14
TOP_Rubber
25 30 4 0
0.5 0.055
000 0
0 2
리지드 파트와 매우 부드러운 초탄성 재질사이의 컨택 문제 때문에 강체 파트 부의 E*h (영률 * 두께)이 고무 물성의 벌크 모듈러스 거의 동일해야 합니다.
RADIOSS Option Used
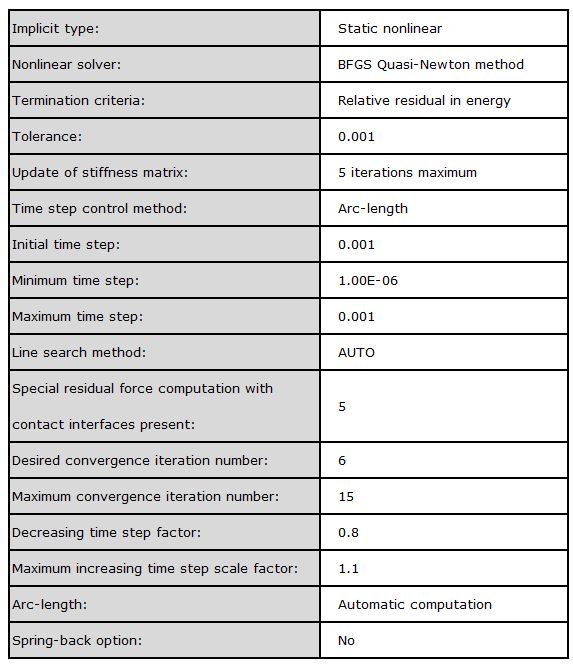
초탄성 그리고 접촉 조건은 주요한 비선형성을 나타냅니다. 그래서 정적 비선형 해석을 arc-length 변위 전략으로 계산했습니다. 이에 대한 타임스텝은 변위 컨트롤로 계산됩니다.
다음은 비선형 Implicit 파라미터 들에 대한 표입니다.
비선형 사이클에 대한 각각의 iteration은 Ax=b의 방정식의 해를 구하기 위해 사용되며, 이를 정의 하는 키워드는 /IMPL/SOLVER입니다.
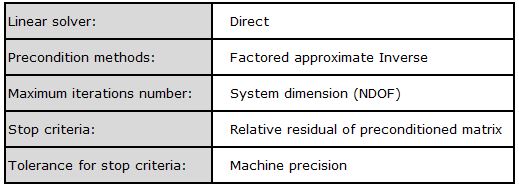
선형 Implicit 옵션은 다음과 같습니다.
두번째 스탭의 해석을 수행하기 위해 엔진 파일을 두개로 구분했습니다.
마지막으로 두 스탭에 대한 엔진 파일은 동일하며 이 파일에 Implicit 키워드들이 포함되어 있습니다.
/IMPL/PRINT/NONLIN/-1 — Printout frequency for nonlinear iteration
/IMPL/NONLIN/2 —- Static nonlinear computation
5 1 0.001
/IMPL/SOLVER/3 —– Solver method (solve Ax=b)
5 0 3 0.0
/IMPL/DTINI —– Initial time step determines initial loading increment
0.001
/IMPL/DT/STOP ——- Min Max values for time step
1e-6 0.001
/IMPL/DT/2 —— Time step control method 2 – Arc-length + Line-search will be used with this method to accelerate and control convergence.
6 0 15 0.8 1.1
/IMPL/AUTOSPC/ALL —- Constraining automatically zero stiffness dof
/IMPL/LSEARCH/3 —- Line search method for nonlinear analysis
/IMPL/RREF/INTER/5 —— Special Reference residual computation with contact
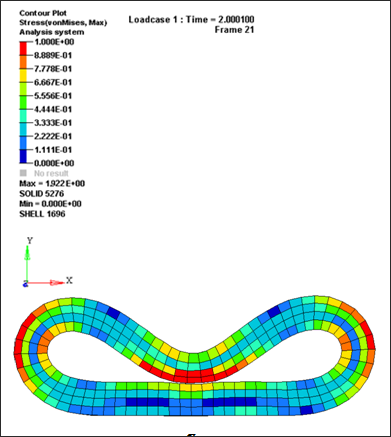
시뮬레이션 결과 및 결론
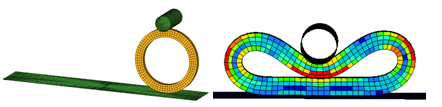
다음은 결과에 대한 이미지입니다.
결론
본 해석은 구체적인 비교 대상이나 기준이 되는 이론식과 같은 것들이 없기 때문에 단순하게 RADIOSS의 Implicit 솔버를 이용하여 비선형 대변형 해석을 한 케이스로 생각하시면 됩니다.
끝
RADIOSS Example 공략 31 – Perfect Gas Modeling with Polynomial EOS
|
<-- 이전 글 보기
|