목적
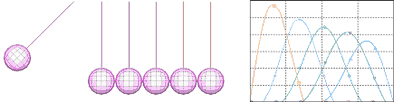
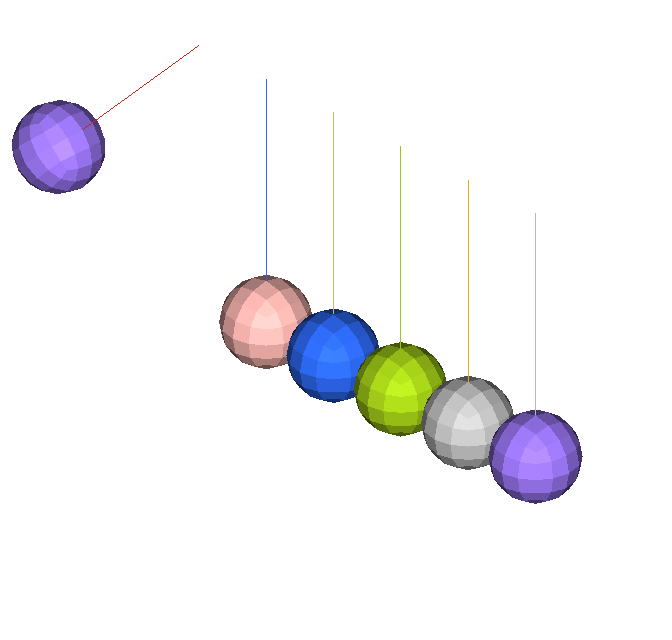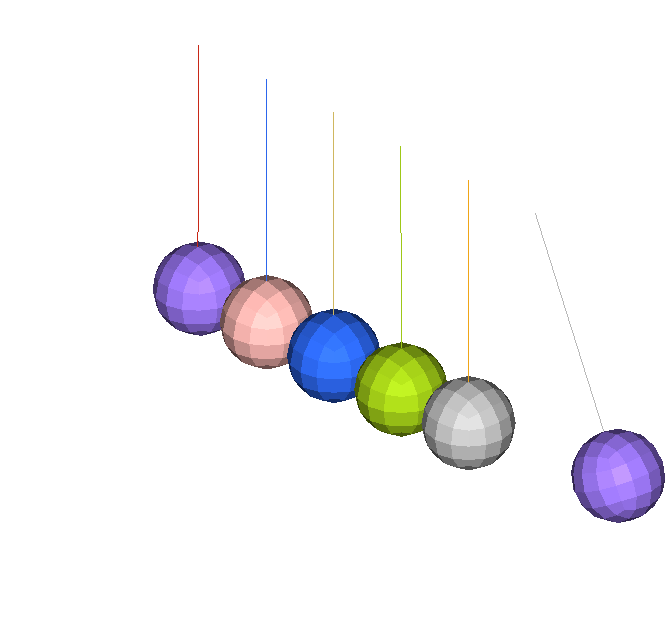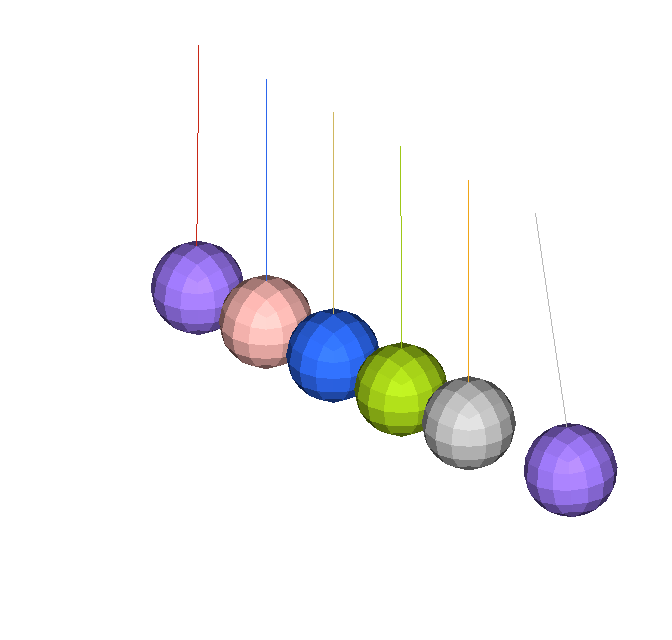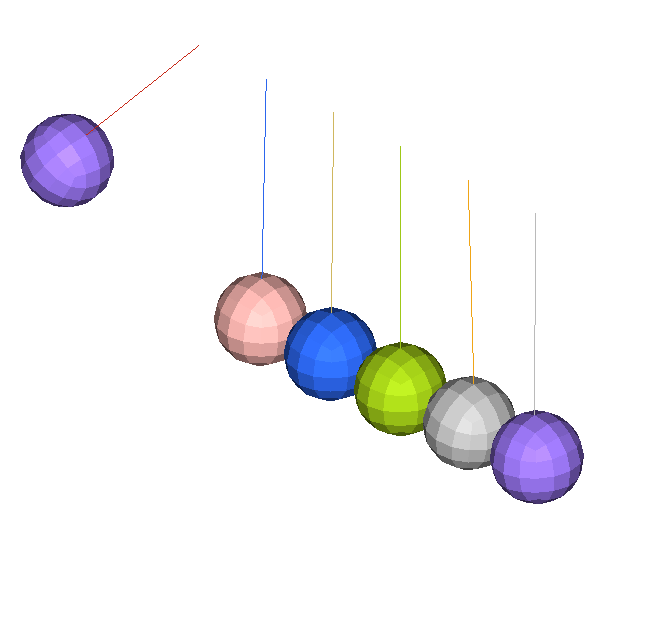
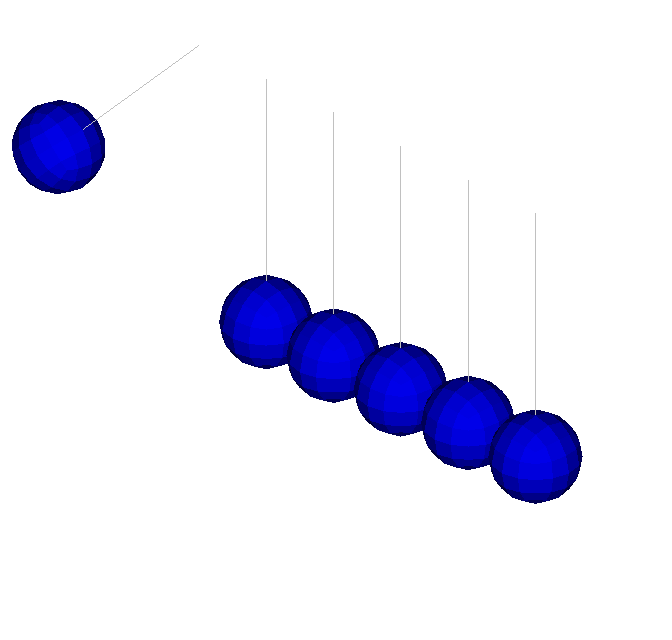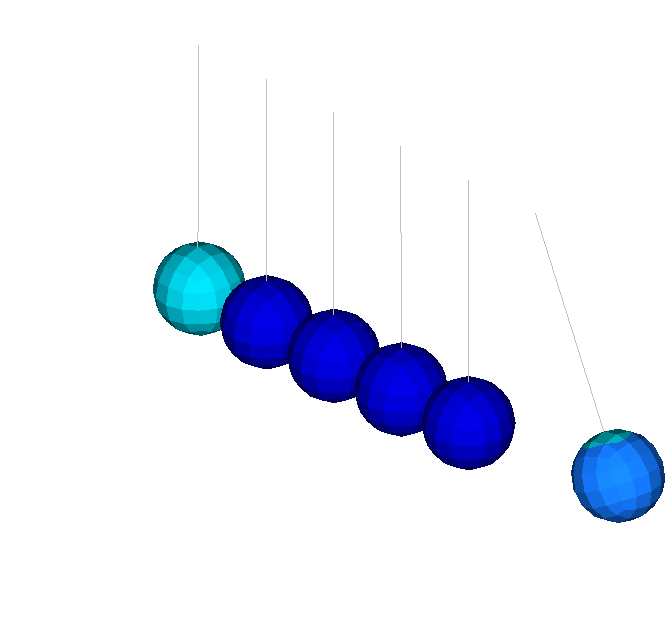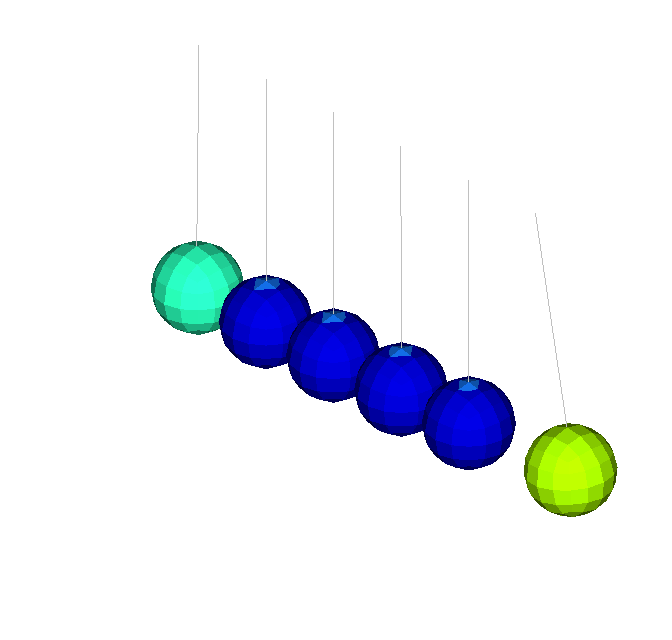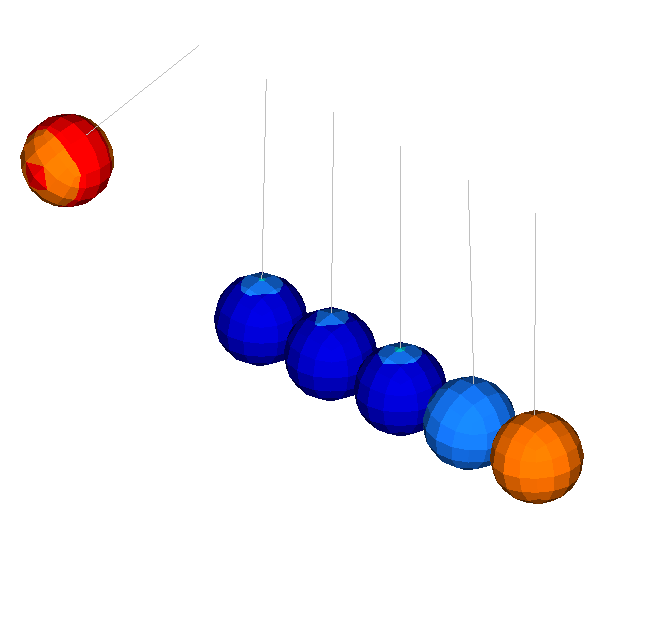
이번 예제의 목적은 여러개의 Pendulum을 통해서 전달되는 충격 웨이브와 운동량을 시뮬레이션으로 확인 하기 위한 것입니다. 충격시 발생하는 동역학적 거동은 3D 요소로 모델링하여 표현하였고, 평면 변형률의 가정은 디테일한 2D 요소로 모델링하여 충격파의 전파와 역학적 접촉을 확인 할 수 있습니다.
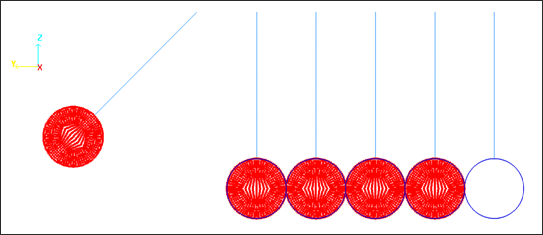
모델에는 중력이 적용되었고 처음 Pendulum이 충격하였을때 6번째 Pendulum까지는 거동의 변화가 없고 마지막 Pendulum에 처음의 거동이 그대로 전달됩니다.
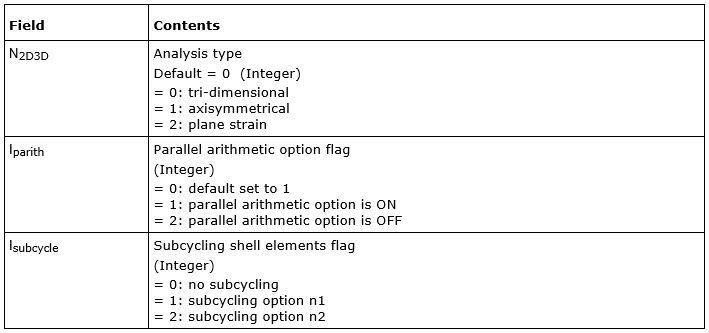
주요 물성 정보
단위 : mm, ms, g, N, MPa
/MAT/LAW1 (elastc material)
Pendulums (알루미늄)
– Initial density : 0.0027 g/mm^3
– Young’s modulus : 70,000 MPa
– Poisson’s ratio : 0.3
Truss
– Length : 124.6 mm
Ball (45도 기울어져 상태)
– Radius : 25.4 mm (mass = 182.5g)
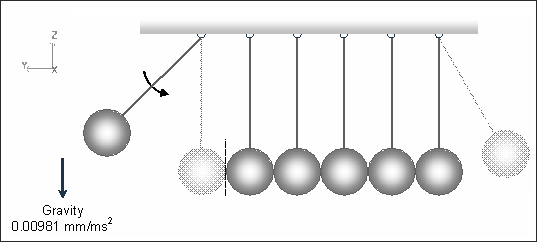
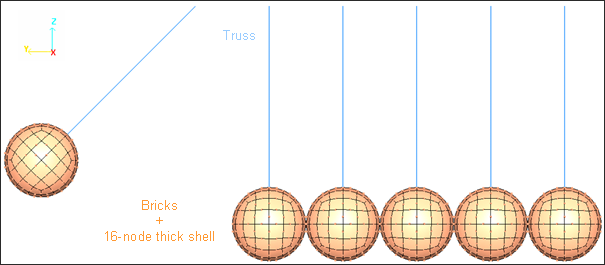
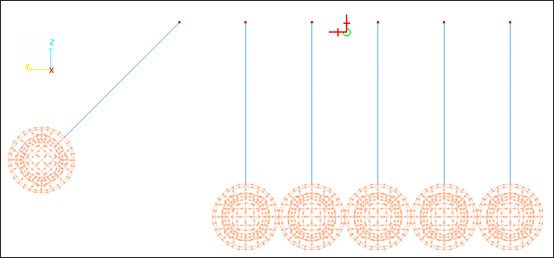
모델링 정보
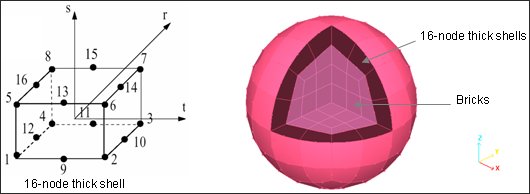
Ball에는 2D와 3D가 동시에 모델링 되어 있습니다. 2D Shell은 16개의 node를 갖고 있는 육각형태로 정의되었으며 내부에는 8 node의 육각 3D solid 요소로 모델링 되었습니다.
접촉 조건에 대한 정의는 Interface 16번의 Lagrange Multipliers 기법이 적용되었으며 Pendulums들 간에 각각 적용되었습니다. type 16번은 접촉 간격의 설정 없이 정확한 컨택 조건을 만족시켜줍니다.
모든 Pendulums에는 /GRAV 카드를 사용하여 중력이 적용되었습니다. (gravity :-0.00981)
Pendulums을 지탱하고 있는 Truss는 dof 2,3,5,6이 고정되어 있습니다.
Y,Z의 병진방향과 Y,Z의 회전 방향에 대한 고정입니다.
평면 변형률에 대한 접근을 적용하기 위해서 2D모델에 /ANALY 카드의 N2D3D 값을 2로 설정했습니다. 2D 요소의 X 축 방향을 평면 변형률 방향으로 지정하였고 Ball에 적용된 요소 한 개당 길이는 0.5mm 입니다.
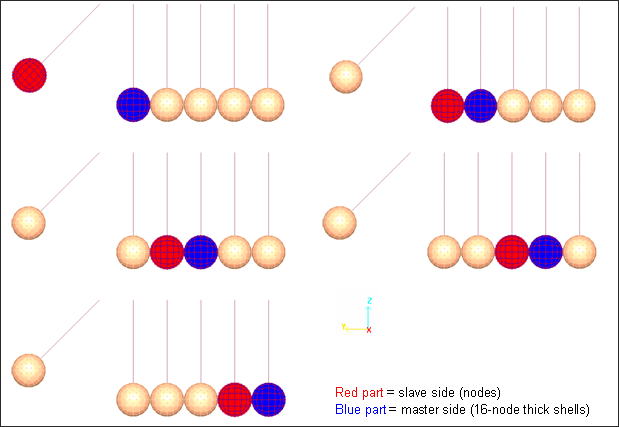
2D 요소의 수직 벡터들은 Negative Volumes이 발생하는 것을 방지하기 위해서 동일한 방향으로 맞춰졌습니다. 충격시 Ball 내부의 요소간의 간섭을 피하기 위해서 type 5 interface를 설정했습니다. interface 5는 아래 그림에 보이는 것과 같이 겉 면을 master (파란색)로 내부를 slave (빨간색)으로 설정했고 접촉의 간격은 0.1mm로 설정되었습니다.
해석 결과
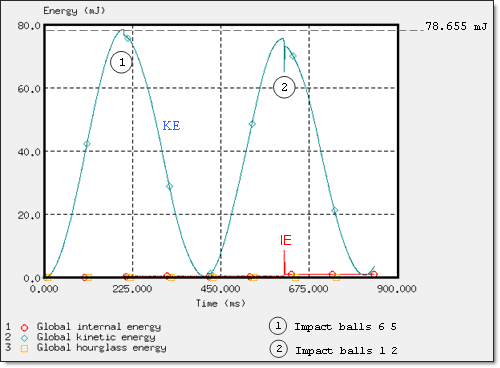
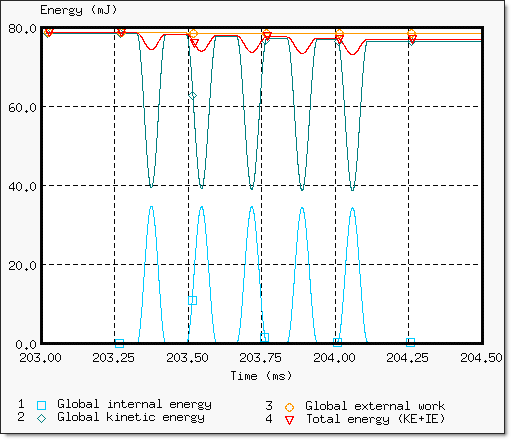
아래 그림은 모델의 운동에너지 변화를 나타내고 있습니다. 그림을 확인해보면 운동에너지의 변화가 단일 pendulum인 것과 같은 거동을 보이고 있습니다.
최대 운동에너지는 h (높이)가 최대일 때 이므로 h 값을 계산해보면 다음과 같다.
h = hmax = I(1 – cos(45)) = 43.934 mm
위의 값을 다음과 같은 이론 공식에 대입하면 아래와 같은 결과를 얻을 수 있다.
이론 결과
EKINETICmax = m*g*h = 182.5 * 0.00981 * 43.934 = 78.656 mJ
시뮬레이션 결과
EKINETICmax = 78.655 mJ (time = 203.33 ms, impact balls 6 and 5)
EKINETICmax = 72.478 mJ (time = 612.5 ms, impact balls 1 and 2)
결과를 확인해보면 운동에너지가 충격이 진행되는 동안 컨택 에너지가 분산되었기 때문에 완전히 보존되지는 않았습니다.
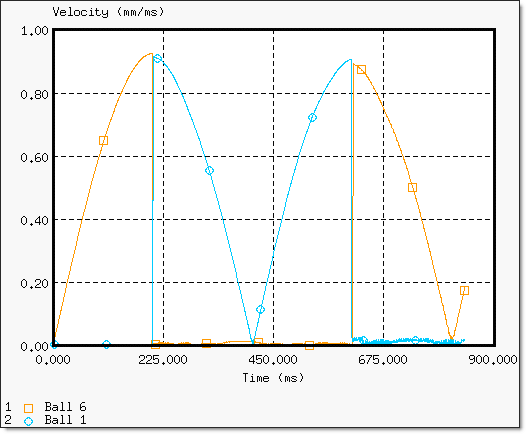
Ball 1과 Ball 6의 pendulum을 봤을 때 충격량이 전달 된 후에 진동이 발생하는 것을 아래 속도 그림에서 확인할 수 있습니다.
충격이 발생 했을 때 (203.33 ms ~ 204.11 ms)의 에너지 거동은 다음과 같습니다.
애니메이션
끝! 자세한 설명이나 모델링 방법은 메일로 문의주시기 바랍니다 ^^
공략 8편 – Hopkinson Bar
|
<-- 이전 글 보기
|
다음 글 보기 –>
|