목적
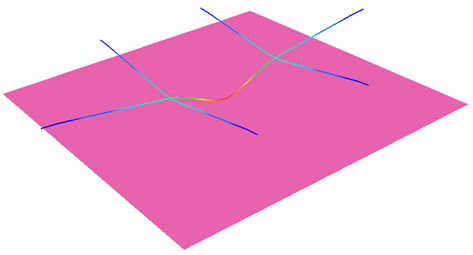
고정된 빔 프레임의 중간 부분에 초기 속도를 가진 매스로 충격을 부여하는 모델입니다. 요소는 Johnson-Cook 탄소성 물성이 적용되었으며 모든 Mesh는 빔으로 구성되어 있습니다. 동적 문제와 Explicit 솔버를 사용하여 이 문제를 해결하는 것이 이번 예제의 목적입니다. Explicit 방식의 접근이 충격 후의 물체의 준 정적 평형 상태를 찾는데 도움을 줍니다.
요약하자면, 이번 예제의 목적은 빔 요소를 이용한 준 정적 해석을 수행하는 것입니다.
본 예제는 초급자 단계로 설명된 내용은 다소 복잡하지만 모델을 보시면 간단한 것임을 확인 할 수 있습니다.
주요 물성 정보
– Initial density : 0.0078 g/mm^3
– Young’s modulus : 200,000 MPa (양방향 모두)
– Poisson’s ratio : 0.3
– Yield stress : 320 MPa
– Hardening parameter : 134.65 MPa
– Hardening exponent : 1.0
다른 모든 상수들은 기본 값으로 들어가며, 소성성의 경우 Law 2를 이용하여 Failure 없이 고려합니다.
유한요소 모델 정보
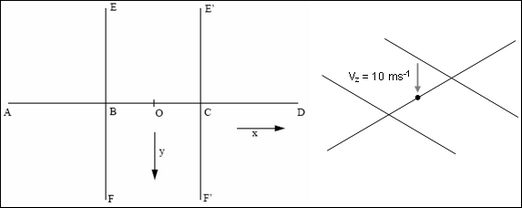
– Dimension : AB = BC = CD = BE = BF = E`C = CF` = 90 mm
– Pixed points (완전 구속 점) : A, D, E, F, E`, F`
Beam information
– Cross section : 36 mm^2
– Moments of inertia in Y and Z : 108 mm^4
– Moments of inertia : 216 mm^4
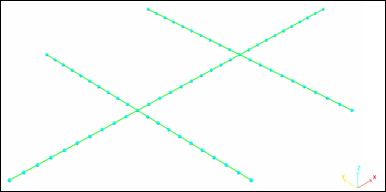
모든 요소는 일반 빔 Mesh를 사용했으며 9mm 간격으로 생성되었습니다. (전체 = 70개의 빔 요소)
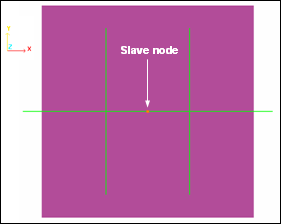
Interface (접촉조건)
Beam 요소의 중간 부분 (Point O) 를 Slave node로 설정되었으며, 다른 부분에는 접촉조건이 고려되지 않았습니다. Rigid wall을 이용한 접촉으로 해당 Slave node만 접촉이 적용됩니다.
해석 결과
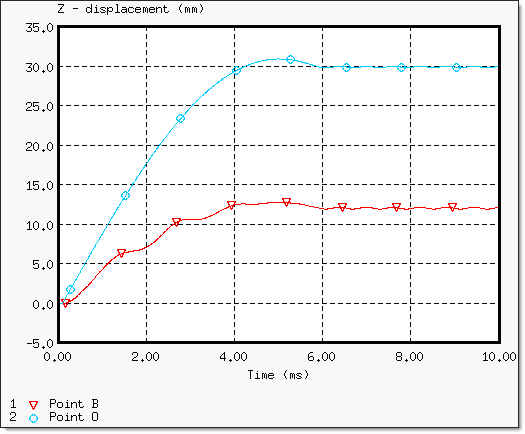
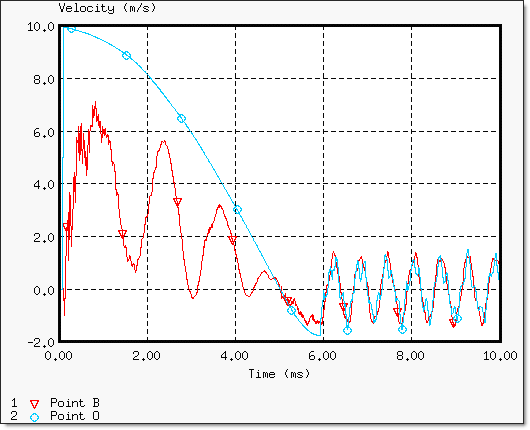
Point B와 O에서의 결과를 Output block을 통해 Graph 데이터로 추출했고 두 점에서의 변위와 속도 변화를 아래 그림에서 참고하시기 바랍니다.
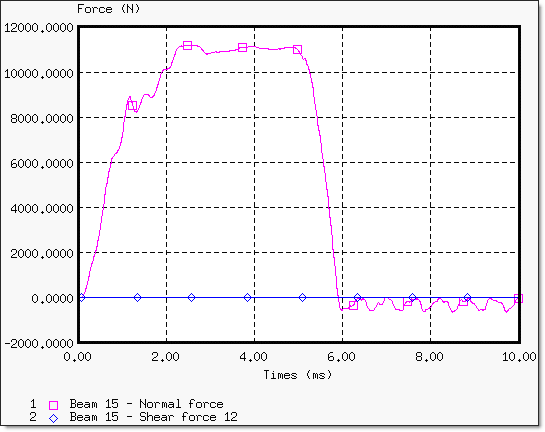
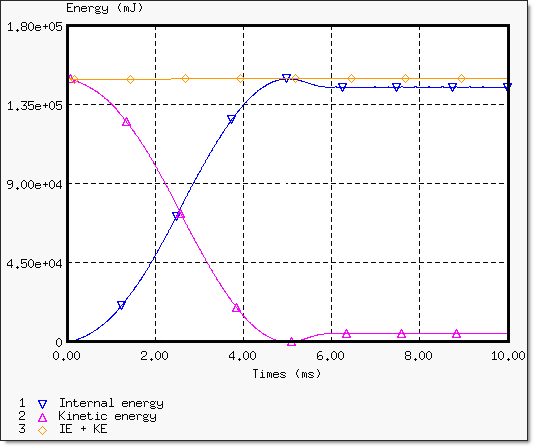
다음은 빔 요소에 작용하는 힘과 에너지 변화에 대한 그래프 결과입니다.
끝! 좀 더 유익한 내용으로 다음 편에서 뵙겠습니다.
공략 6.1편 – Feul Tank
|
<-- 이전 글 보기
|
다음 글 보기 –>
|