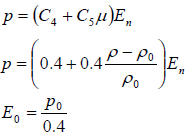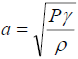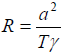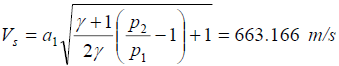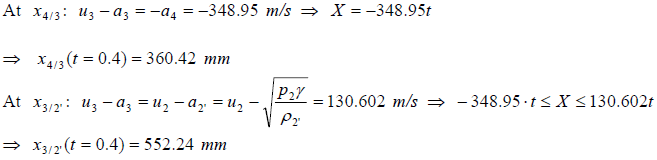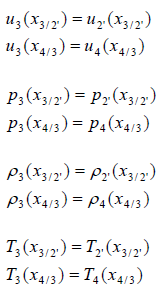목적
충격파를 관찰하기 위한 유명한 실험인 리만 문제의 Shock Tube에 대한 RADIOSS 예제입니다. 이번 예제에서는 이상기체에 대한 여러가지 계산 방식을 적용하여 결과를 비교합니다.
예제 개요
시작하기에 앞서서 이상기체 묘사를 위한 모델링에 대해서 알아봅니다. 본 예제에서는 이상기체 묘사를 위해 LAW6 (hydrodynamic viscous fluid) 물성이 사용되었고, 라그랑지안과 오일러리안 방식을 적용하여 결과를 비교합니다. 둘의 대표적인 차이점은 다음과 같습니다.
Lagrangian (Mesh의 포인트가 물성의 포인트와 일치)
Eulerian (Mesh의 포인트가 고정되어 있음)
오일러 방식은 단계별로 다른 Time Step scale factor가 적용됩니다.
두 ALE 기법과 별개로 본 예제에 사용되는 SPH에 대해서 설명하자면, 격자 형태의 Mesh가 존재하지 않는 SPH 요소는 볼륨 전체에 균일한 간격으로 입자를 분배하는 형태의 모델링입니다.
정리하자면 본 예제에서는 ALE (오일러, 라그랑즈)와 SPH 총 3개의 모델의 결과를 비교 분석합니다.
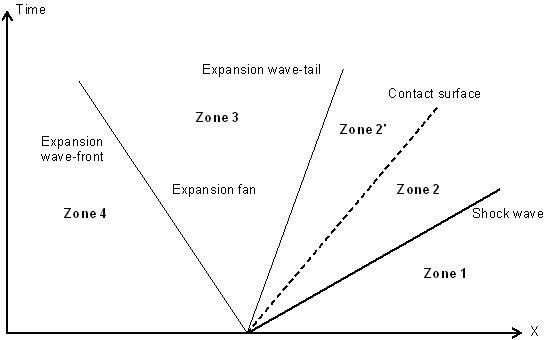
본 예제는 관내에서의 기체의 파동을 분석적인 방법으로 스터디합니다. 기체는 확장 웨이브로 묘사된 별도의 파트로 구분되어 있으며 충격부와 접촉면으로 되어있습니다.
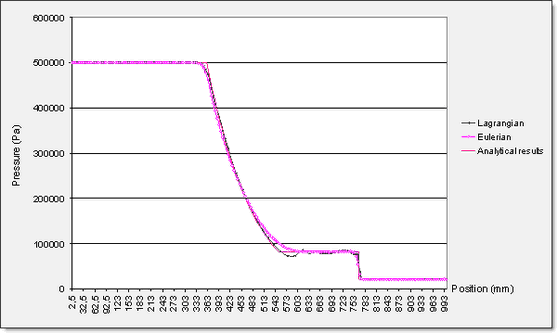
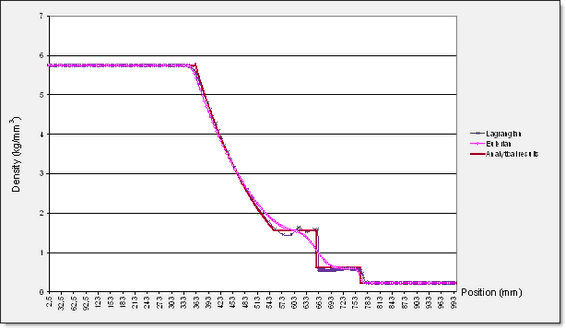
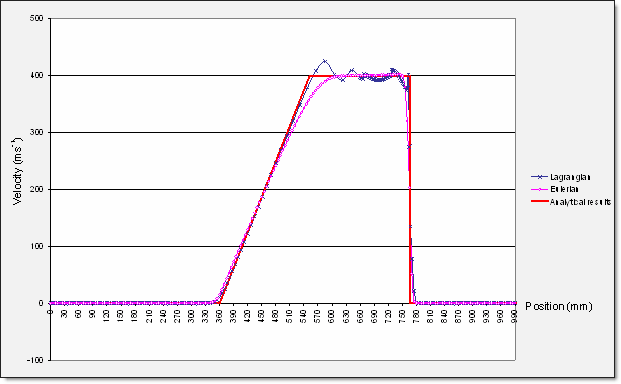
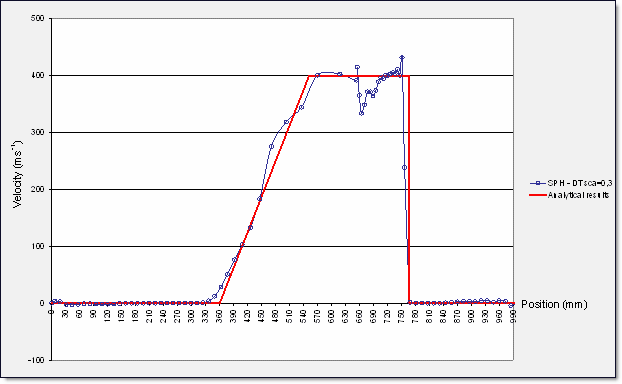
각각의 시뮬레이션 결과는 속도와 밀도 그리고 압력에 대한 분석으로 비교합니다.
예제의 목적
Shock Tube 문제는 기체 동역학에서 다루는 기본적인 문제중에 하나입니다. 문제에 대한 정확한 해결 방법이 있고 이를 시뮬레이션 결과와 비교 할 수 있어서 매우 흥미로운 예제로 여겨지고 있습니다. 시뮬레이션은 SPH 방법과 ALE(오일러, 라그랑즈)가 사용된 유한요소법으로 수치해석적인 접근이 가능합니다.
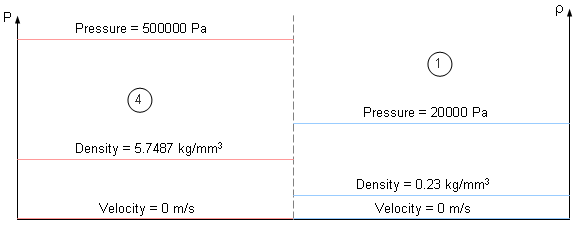
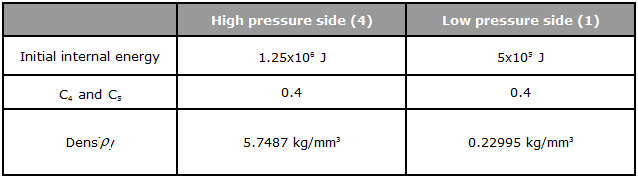
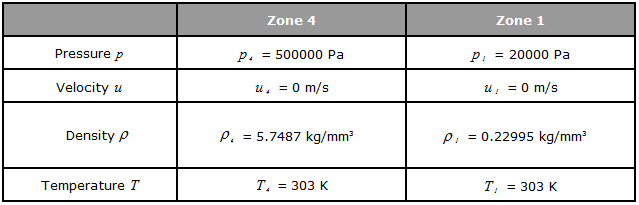
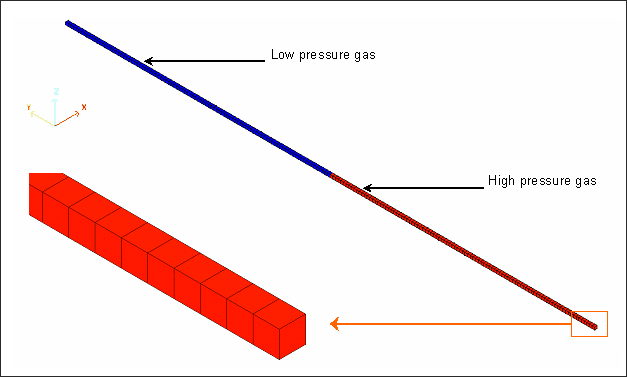
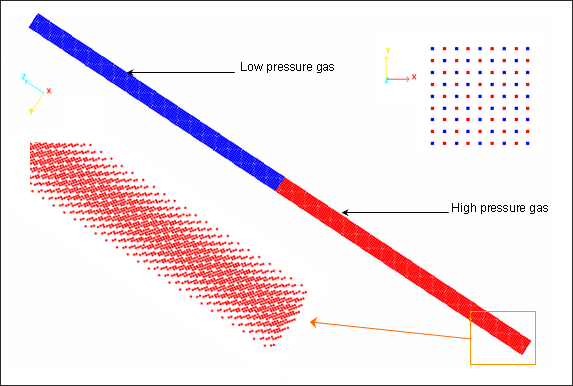
Shock Tube는 두개의 다른 물리적 상태지만 동일한 기체가 채워져있는 긴 관 형태로 구성되어있습니다. 다이아그램을 기준으로 분리된 두개의 파트로 모델이 구분되어있습니다. 초기 상태는 아래 그림에 보이는 것 처럼 밀도, 압력 그리고 속도의 값으로 정의되어있습니다.
모든 점성 효과(유속에 영향을 주는)는 튜브의 측면을 따라서 주지만, 매우 작아서 무시할수 있습니다. 그리고 시작점의 움직임이 없다는 것 또한 모델에서 고려해야 합니다.
(Shock Tube의 스케치)
(불연속적인 초기 상태)
그림에 보이는 것처럼 시작점 t=0 에서의 상태는 압력과 밀도차는 존재하지만 속도는 0입니다.
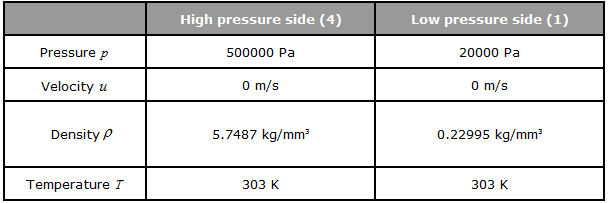
자세한 초기 조건은 아래와 같습니다.
멤브레인이 제거된 후에, 저밀도파가 관내의 고압력 영역으로 이동하는 동안 압축 충격이 압력이 낮은 영역으로 이동하게되며, 이때 대체로 접촉의 단절이 발생하게 됩니다.
분석 / 가정 / 모델링 묘사
- RADIOSS에서의 이상기체 모델링
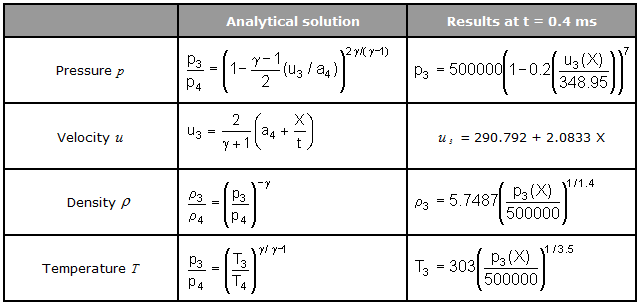
LAW6(hydrodynamic viscous fluid)는 압축 기체를 묘사 할 때 사용됩니다.
해당 물성의 압력에 대한 방정식은 다음과 같으며,
점성 계수는 다음과 같은 관계식을 갖습니다.
이와 같은 조건일 때 p는 압력, Ci는 hydrodynamic 상수, En은 단위 체적당 내부에너지 로는 밀도입니다. 이상 기체는 사용되어지는 coefficient C0, C1, C2 그리고 C3가 0으로 묘사되어지며 또한 C4 = C4 = 
– lc입니다. 여기서 는 기체 상수를 뜻합니다.
단위 체적당 초기 내부에너지는 아래 방정식과 초기 압력으로 부터 계산 할 수 있습니다.
기체상수 = Cst = 1.4 (저온 상태에서 유효)라는 가정하에 hydrodynamic 상수 C4, C5는 동일하게 0.4로 설정합니다.
기체 압력은 아래와 같이 묘사되어지며,
LAW6 물성의 파라미터들이 아래 표와 같이 제공됩니다.
분석 접근
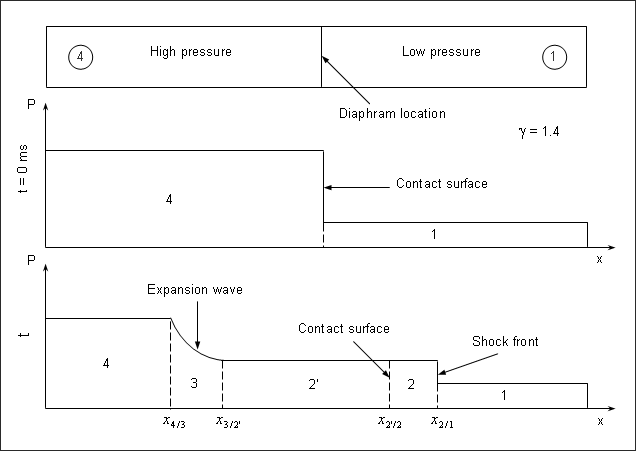(다이아그램 제거 전 후의 압력 분배에 대한 shock tube 문제 개략도)
흐름 패턴의 변화를 위 그림에서 확인 할 수 있습니다. 다이아그램이 깨졌을 때 고압력, 저압력 사이의 연결성이 깨지면서 웨이브가 좌측, 우측 각각의 방향으로 이동합니다. 각 웨이브 패턴은 중앙부와 충격 또는 저주파의 접촉 단절로 구성되어 있습니다. 충격파는 초음속의 속도로 저압력 영역에 단일 방향으로 진입하게 됩니다.
(충격, 확산파와 접촉면에 대한 다이아그램)
4개의 확실하게 구분되는 영역을 그림에서 확인 할 수 있습니다.
영역 1은 저압력 상태의 기체로 충격파가 전이되지 않는 상태이며 영역2 (2와 2`로 구분된)는 충격 직후 일정 속도로 움직이는 기체를 포함하고 있습니다. 영역2에 존재하는 접촉 면은 밀도와 온도가 불연속적인 영역에 가로질러서 놓여있습니다.
영역3은 expansion fan의 머리와 꼬리부분 사이에 위치합니다. 여기서는 확산 과정이 등엔트로피 상태이기 때문에 흐름 특성이 점진적으로 변하게 됩니다. 영역4는 고압력 기체가 분배되지 않는 상태를 보여줍니다.
영역2에서의 관계식은 The normal shock relations를 이용해서 얻을 수 있고, 압력과 속도는 영역 2와 2’에서 동일합니다.
기체상수 에 대한 비열의 비율은 1.4로 고정되어있으며 이는 온도의 영향(저온 상태)으로 값이 변하지 않는다는 가정하에 정의됩니다.
리만 문제에 대한 해석적인 해결방법은 시간이 0.4ms일 때 나타납니다. 해답은 구분된 영역에 따라서 얻어지며 반드시 연속성을 확인해야 합니다.
영역 2와 영역3에서의 변화는 영역1과 영역4의 일정한 조건에 의존적입니다. 해석 방정식의 변수로 압력, 속도, 밀도, 온도, 사운드 스피드가 있으며 이들은 기체와 특정 기체상수를 통해서 사용됩니다. 영역 2에서의 방정식은 끝까지 일정합니다.
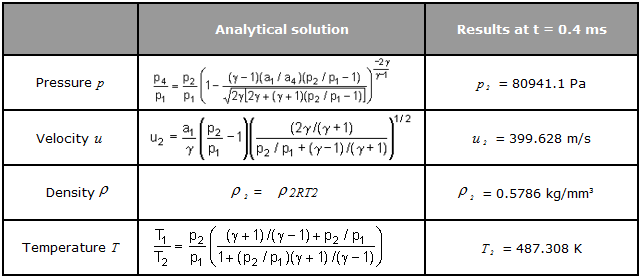
충격파와 접촉면의 속도는 영역 한계의 위치를 정의 할 수 있도록 합니다.
영역4와 영역1의 정보
기체의 사운드 스피드
특정 기체 상수
영역2의 정보
충격파 속도
따라서 x2/1 = Vs * 0.4 + 500 = 765.266 mm
영역 3의 정보
영역 3은 다음과 같의 정의됩니다.
x = 500 + X 일 때,
연속성 정의 :
라그랑즈과 오일러 방법의 유한요소 모델링
기체는 200개의 ALE brick 요소로 구성되어 있으며, solid property 14를 사용합니다.
각 brick 요소의 크기는 5 mm x 5mm x 5mm 입니다.
(라그랑즈, 오일러 접근 방식의 Mesh)
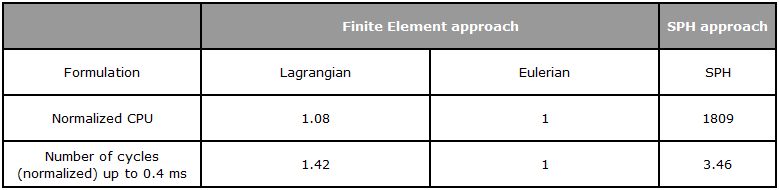
라그랑즈 방법에서 Mesh의 포인트는 물성의 포인트와 동일하게 위치하며 요소의 변형 또한 물성과 함께합니다. 요쇼가 변형 될 때의 정확성과 Time Step의 감소 때문에, 큰 변형이 발생하게 될 수록 결과가 좋지 않습니다.
오일러 방법에서는 요소의 절점 좌표가 고정되어 있습니다. 절점은 특정한 위치에 고정되게 됩니다. 물성의 변형에 의해서 요소가 변하지 않기 때문에 큰 변형에도 결과의 변동이 없습니다.
두 방법을 비교했을때 오일러 방법이 더 좋은 결과를 제공하는 듯 하지만, 라그랑지안은 해결 방정식을 고려하기 때문에 오일러 접근 방식에 비해 더 좋은 결과를 제공합니다.
ALE 경계 조건은 /ALE/BCS로 정의되며 아래 두 조건을 구속합니다.
- Material Velocity
- Grid Velocity
극점에서의 절점은 material velocty를 갖고 있으며 이는 X와 Z방향으로 고정되어있습니다. 다른 절점들은 X, Y, Z방향으로 고정된 material velocity를 갖고 있습니다.
ALE 물성은 오일러 또는 라그랑즈 방법으로 /ALE/MAT에 정의되어야 합니다.
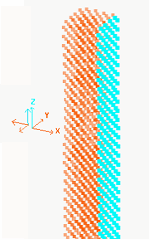
SPH (Smooth Particle Hydrodynamics) 모델링
아래 그림과 같이 총 12798개의 입자들이 Mesh 형상이 아닌 형태로 분배되어 있으며 이러한 형태를 SPH라고 합니다.
(모델링된 SPH 요소의 모습)
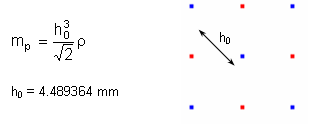
수직 값 h0는 각각의 입자들간 간격을 의미하며 가장 가까운 입자와의 거리를 뜻합니다. 파트에 할당된 속성에 따라서 입자의 질량이 계산되어집니다.
질량은 밀도와 입자의 크기에 관계있으며 정확한 관계식은 아래와 같습니다.
이에 기반하여, 저압력 파트의 입자 질량 mp는 1.25265×10-5g 이고
고압력 파트에서의 mp는 3.13166×10-4g 입니다.
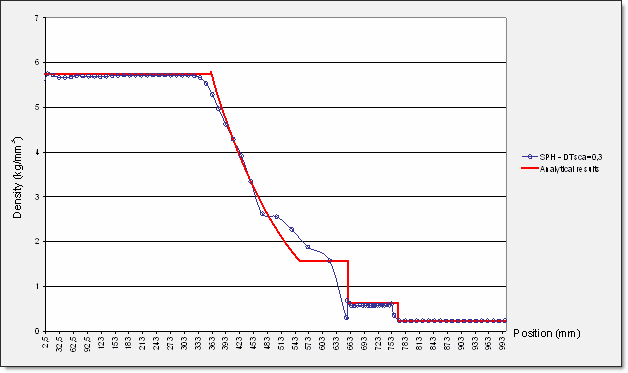
Time Step에 대한 scale factor는 계산의 안정성을 위해 0.3으로 설정했습니다.
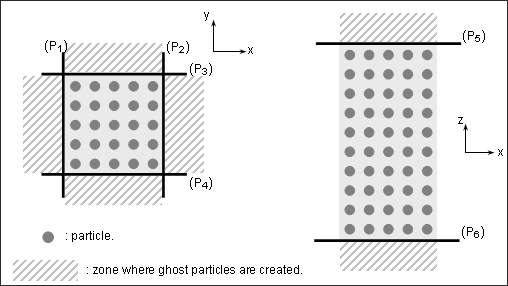
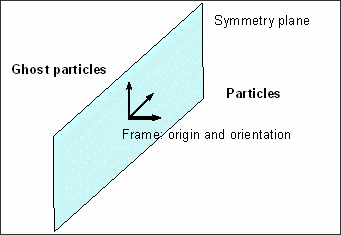
SPH 대칭을 주기 위해 경계 조건을 설정했고 (/SPHBCS) 이 옵션은 SPH 모델링을 정의하고 고스트 입자를 생성하기 위해 정의했습니다. 여기서 고스트 입자는 실제 파트에 대칭이 되어 생성되는 부분을 뜻합니다.
(SPH 대칭 평면 정의)
각 대칭조건은 평면에 부착된 프레임의 원점을 통과하는 평면에 따르거나 이런 프레임의 로컬에 수직한 평면에 따라서 정의됩니다. 선택된 절점과 SPH 대칭조건은 -X 축에 따라서 정의됩니다.
6개의 대칭 평면이 사용됩니다.
x와 -x 대칭 조건 : 리바운드 없는 SLIDE (Ilev = 0)
y와 -y 대칭 조건 : 리바운드 없는 SLIDE (Ilev = 0)
z와 -z 대칭 조건 : 탄성 리바운드가 있는 TIED (Ilev = 1)
SLIDE 조건이 설정된 경우에, 완전히 평면을 따라서 미끄러지게 됩니다.
시간 t = 0 일때, 입자는 반드시 대칭 평면에 위치해야 합니다.
(프레임의 로컬 방향)
입자는 다음과 같이 정의된 positive semi-space로 이동하게 됩니다.
여기서 O는 프레임의 원점이며 P는 평면의 포인트 그리고 N은 프레임의 로컬 방향입니다.
시뮬레이션 결과
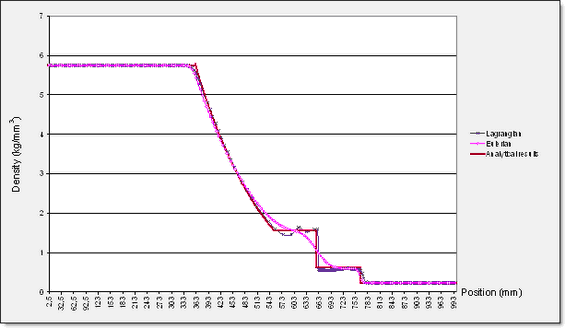
관의 축 방향으로 0.4ms의 시간이 지났을때 시뮬레이션 결과
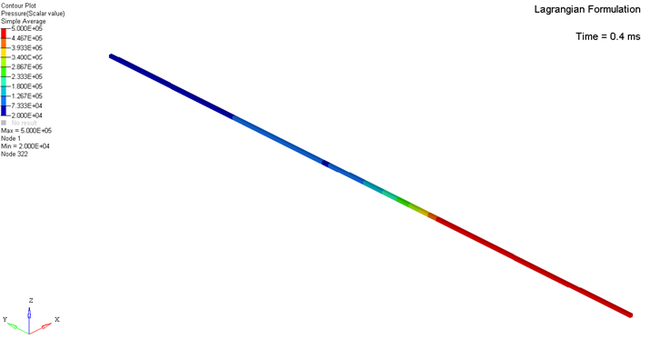
라그랑즈 방법 : scale factor = 0.1
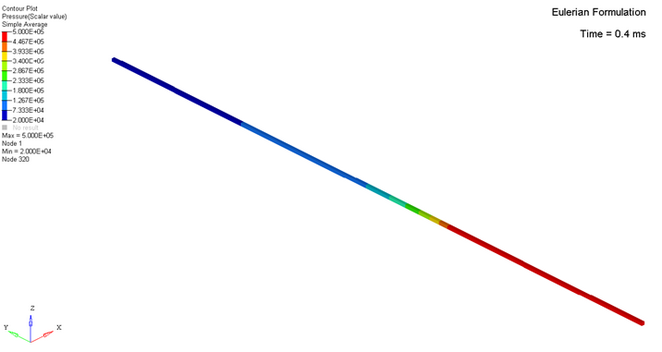
오일러 방법 : scale factor = 0.5
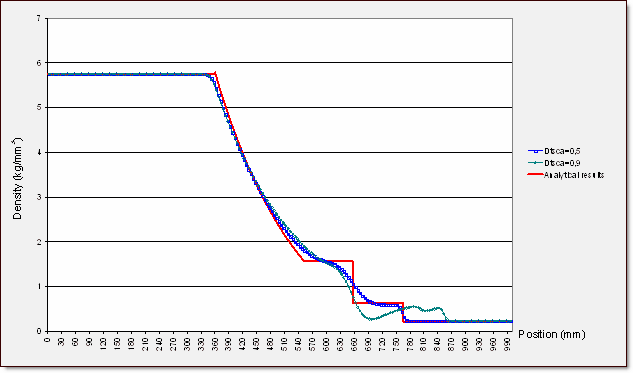
Scale factor 에 따른 결과 차이
Case 1 : scale factor = 0.5
Case 2 : scale factor = 0.9
SPH 결과와의 비교
scale factor를 0.5로 동일하게 두었을 때 각 방법에 따른 계산 결과(CPU)
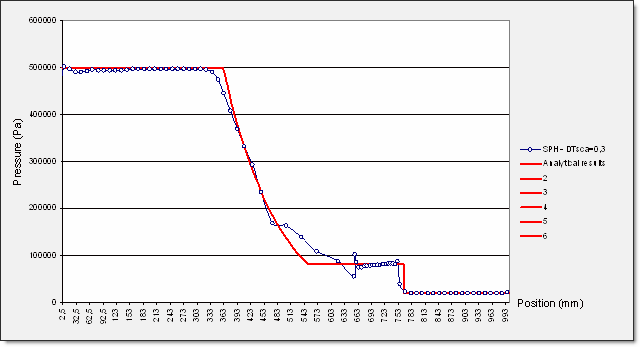
0.4ms에서의 압력 분배 결과
끝.
공략 14.1편 – VPG with a Complete Finite Element Model
|
<-- 이전 글 보기
|
다음 글 보기 –>
|