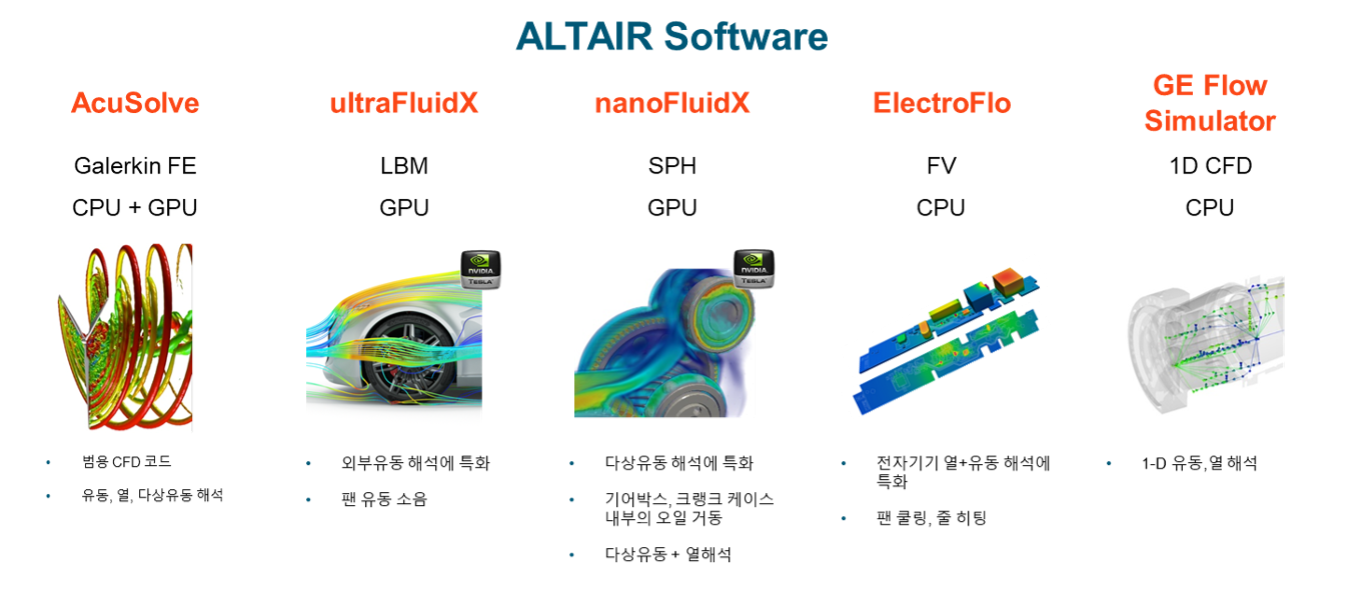
유체역학은 나비에-스토크방정식, 연속방정식, 에너지보존에 관련식과 물성치들의 관계를 통해 물리적인 문제들을 기술합니다.
복잡한 유체의 흐름은 비선형 방정식으로 그 해를 구하기가 매우 어렵고, 많은 실험으로도 결과를 얻어내기 힘든 경우가 있습니다.
이러한 문제를 해결하기 위해, CAE(Computer Added Engineering) 즉, Computer를 이용한 연구 개발방법이 널리 이용되고 있습니다. CFD(Computational Fluid Dynamics)는 컴퓨터를 이용한 열 및 유체유동에 대한 수치적 연구입니다. 또한 CFD는 나비에-스토크방정식에 근간한 수학적 지배방정식들을 수치해석적인 방법으로 접근하여 유동, 열 및 물질전달, 화학반응 등을 해석하는 분야를 뜻합니다.
1) CFD의 역사
유체 역학에 대한 연구는 수세기 전에 이루어졌지만, 대부분의 CFD 관점에서의 발전은 20세기 전반에 걸쳐 이루어졌습니다. 1950년대 이전의 주요 관점은 수치 해석적 솔루션 개발과 함께, 압축성 흐름 계산과 점성 경계층 계산을 위한 다양한 근사 기술을 개발하는 것이었습니다. 1950년대까지는 계산 능력의 한계로 인해 제한된 편미분 방정식에 대한 솔루션만을 제공했습니다. 이후 디지털 컴퓨터의 출현과 성능 향상을 기반으로 50, 60년대에 비점성 압축성 유동의 솔루션에 대한 중요한 발전이 이루어졌습니다.
90년대에는 본격적인 병렬 컴퓨터의 연산 능력 향상에 의해 난류 해석이 활발히 이뤄졌습니다. 난류는 모델링 없이 직접 수치 시뮬레이션(DNS)과 함께 RANS(Reynolds-averaged Navier Stokes) 및 LES(대형 와류 시뮬레이션)와 같은 난류 모델링 기술을 사용하여 통합되었습니다. 또한 CFD 해석 및 도출한 수치 데이터를 시각화 할 수 있는 다양한 상용 소프트웨어들이 등장합니다.
2) CFD의 장점
– 새로운 설계에 대한 시간 및 비용 감소
– 거대하고 복잡한 시스템, 제어가 어렵고 불가능한 실험을 연구할 수 있음
– 안전성 연구 및 위험한 사고 시나리오 등과 같이 정상적인 성능한계 이상에서의 위험한 조건을 연구할 수 있음
– 실제적으로 제한 없이 상세한 결과를 획득
3) CFD의 적용 분야
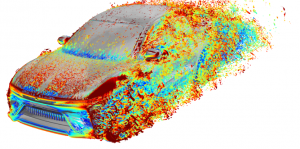
– 항공기 및 자동차의 공기역학 분야
– 빌딩 내외부 환경
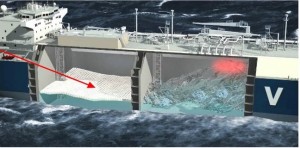
– 선박의 수력학
– 발전소
– 유체기계
– 화학공정공학
4) CFD의 구조
5) CFD Software
감사합니다.
한국알테어