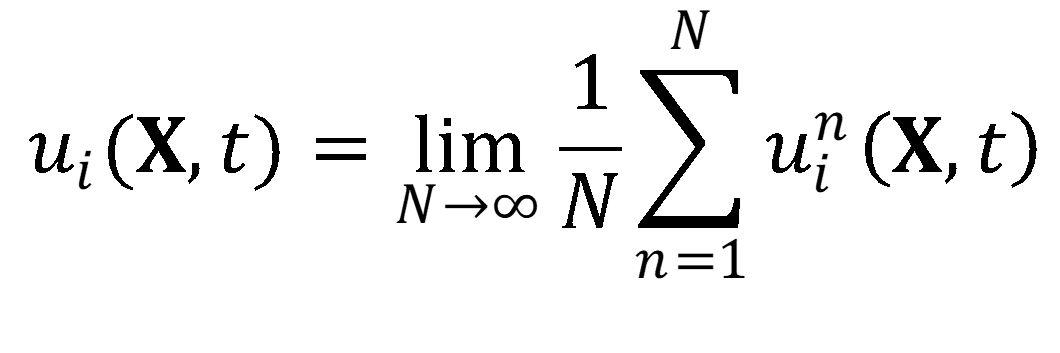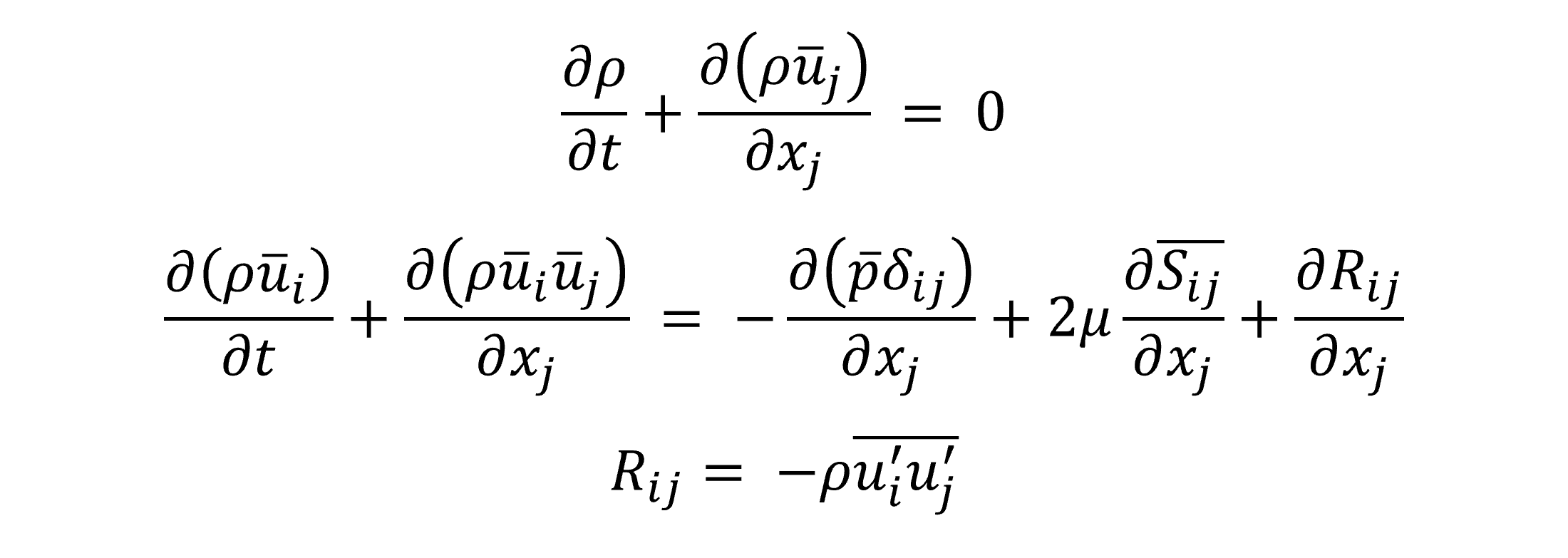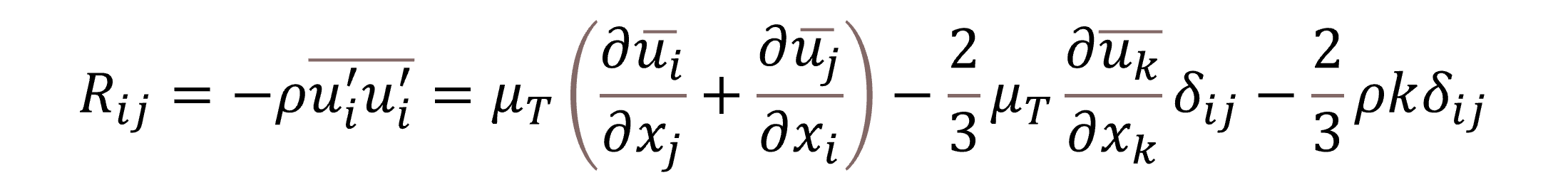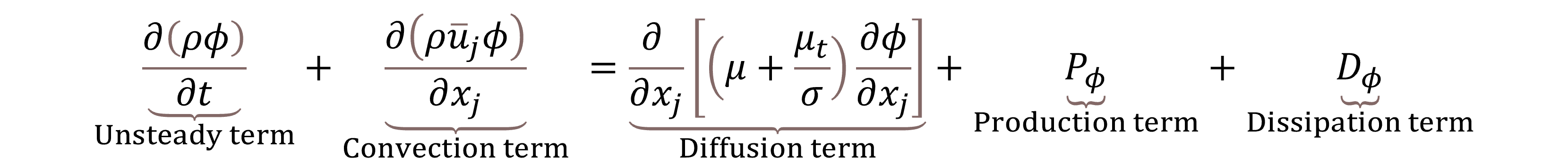난류 모델 2
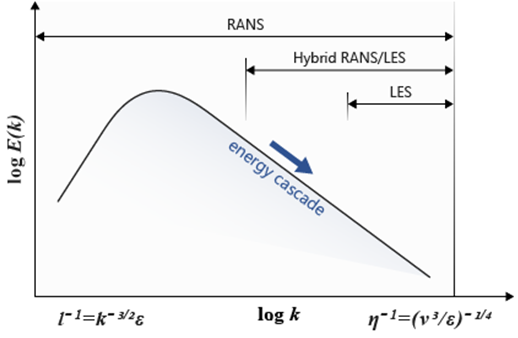
산업체의 유체역학적 메커니즘은 대부분 난류 유동입니다. 난류 모델이 필요한 이유는 엔지니어링 설계에 필요한 유체의 매개 변수(압력강하, 벽 전단력 등)를 구해야 난류의 복잡한 문제를 해결할 수 있습니다. 난류 거동은 시간에 따라 불규칙하게 변화하기 때문에 수치해석적 접근으로 난류 문제를 해결해야 합니다. 난류 유동의 수치해석적 방법으로는 레이놀즈 평균 운동방정식(RANS: Reynolds-Averaged Navier-Stokes equation)에 기초한 RANS 모델을 이용하는 방법과 큰 에디 모사(LES: Large Eddy Simulation)와 직접 수치 모사(DNS: Direct Numerical Simulation) 방법이 있습니다. DNS와 LES방법이 난류거동을 정확히 예측할 수 있지만, DNS의 경우 모든 크기의 에디를 모사하고 LES는 큰 와류들을 실시간으로 해석을 수행하기 때문에 많은 계산 시간이 필요합니다. RANS 모델의 경우 DNS, LES 모델보다 정확도가 떨어질 수 있지만 해석 시간이 빠르고 수치안정성이 좋기 때문에 산업분야에서 많이들 사용하고 있습니다.
1) 직접수치모사 (DNS: Direct Numerical Simulation)
직접 수치 모사 기법(DNS: Direct Numerical Simulation)은 난류 모델을 사용하지 않고 나비에-스토크스 방정식을 직접 수치 해석하여 시간과 공간을 가장 작은 스케일까지 모사하는 방법입니다. 직접 수치 모사에서는 에디의 형태를 모두 모델링 없이 직접 모사하므로 격자의 크기가 가장 작은 스케일인 Kolmogorov의 길이 스케일보다 작아야 합니다. 그래서 해석 시간이 길고 많은 CPU 및 슈퍼컴퓨터가 필요합니다. 또한 격자의 크기가 작지 않을 경우 난류의 작은 스케일에서 발생하는 소산을 정확히 예측할 수 없어 유동현상을 제대로 예측하지 못하게 됩니다.
2) 큰 에디 모사 (LES: Large Eddy Simulation)
큰 에디 모사는 격자보다 큰 스케일의 에디만을 직접 계산하며, 격자 보다 작은 스케일의 에디에 대해서는 모델링을 통하여 계산하는 방법입니다. 결국 DNS와 RANS 모델의 중간 기법이라 생각하면 됩니다. 난류 현상에서 작은 스케일의 난류는 유동형태의 변화에 크게 관여하지 않습니다. LES에 필요한 격자 수는 DNS에 비하여 적기 때문에 실제 현상에 적용이 가능합니다. 그리고 유동에 직접 영향을 미치는 큰 에디를 직접 계산하기 때문에 RANS 모델 보다 예측 성능이 뛰어납니다. 하지만 RANS 모델에 비해 격자수가 많이 필요하고, Transient 해석을 수행해야 하기 때문에 해석시간이 상당히 소요됩니다.
3) 레이놀즈 평균 운동방정식 (RANS: Reynolds-Averaged Navier-Stokes equation)
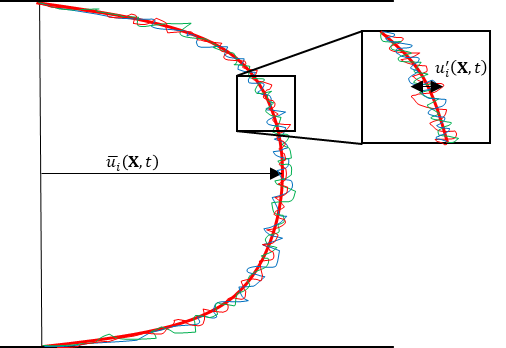
난류는 섭동(fluctuation) 때문에 속도와 압력이 시간과 공간에 따라 변화하게 됩니다. 그래서 연속 방정식과 운동량 방정식에서 해를 구할 수 없어 난류를 평균 함수로 나타냅니다. 순간 또는 난류 속도의 함수(Instantaneous component)는 시간평균의 함수(Time-average component)와 섭동(Fluctuating component)의 합으로 정의할 수 있습니다.
섭동 성분을 운동량 방정식(Navier-Stokes Equation)에 적용하면 다음과 같이 레이놀즈 평균 운동량 방정식 형태로 나타낼 수 있습니다. 여기서 Rij는 레이놀즈 응력(Reynolds stress)이라고 부르며, 난류 모델이란 레이놀즈 응력을 구할 수 있는 모델링을 말합니다.
즉, 난류 모델이란 레이놀즈 평균 방정식(RANS)에서 레이놀즈 항과 유속 성분들을 계산하는 모델을 제공하여 레이놀즈 평균 방정식(RANS)을 닫는 모델을 말합니다. 난류 모델에는 와류 점성 난류 모델(Eddy viscosity model)과 레이놀즈 응력 모델(Reynolds stress model)이 있습니다. 와류 점성 난류 모델은 레이놀즈 응력 모델의 특수 형태입니다.
레이놀즈 응력 모델은 난류에 의해 발생되는 난류 점성계수를 가정하지 않고 수송방정식으로부터 구하는 방법입니다. 이 접근 방법은 복잡한 유동장에서 변동율, 체적력 그리고 방향성의 영향 등을 실질적으로 고려하지만 수렴성이 좋지 않은 단점이 있습니다.
와류 점성 난류 모델은 작은 와류로 구성된 난류가 계속적으로 형성되고 소산되는 것을 가정합니다. 여기서 레이놀즈 응력은 평균 속도 구배에 비례한다고 가정합니다. 이것을 와류 점성 가정이라고 하며 다음과 같이 모델링 하는 것을 와류 점성 난류 모델이라고 합니다.
여기서 μt는 와류 점성도를 나타내며, 레이놀즈 응력은 난류 점성도와 속도 구배의 함수로 나타납니다. 이러한 와류 점성 모델을 활용하면 RANS 방정식은 다음과 같이 정의될 수 있습니다.
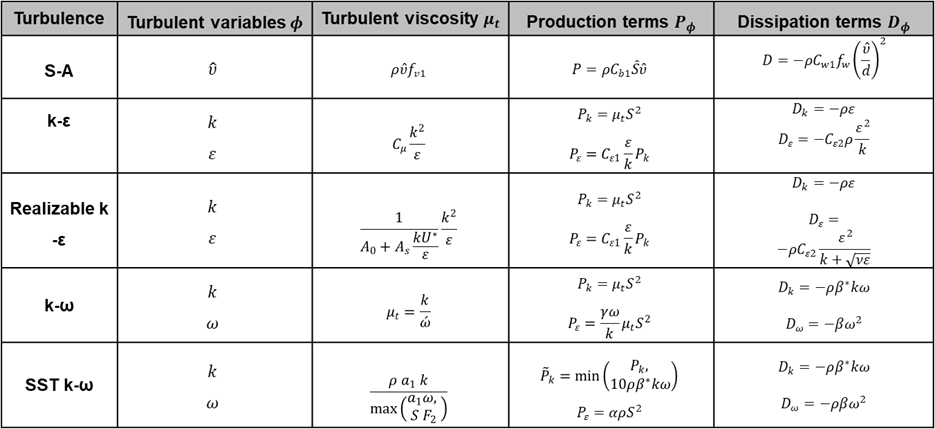
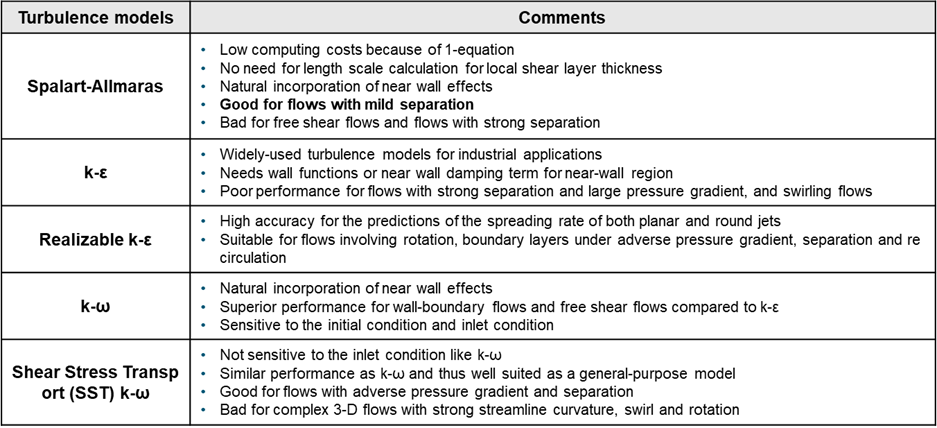
난류 점성계수를 구하기 위해 난류 모델 전달 방정식의 수에 따라 구분하면 0 방정식, 1 방정식, 2 방정식 모델로 구분하는데 전달 방정식의 수가 증가할수록 수치해를 얻기 위한 계산시간이 길어지며 난류 모델의 예측성을 높일 수 있게 됩니다.
0 방정식 모델은 일반적으로 혼합 거리 모델이라 부르며 이는 차원 해석에 의해 적어도 하나의 속도 스케일 및 길이 스케일이 사용됩니다. 혼합거리 모델은 Prandtl에 의해 처음으로 제안 되었습니다. 그리고 1 방정식 및 2 방정식 모델은 하기 표에 정리하였습니다.
다음 시간에는 벽함수와 y+의 개념을 알아보겠습니다.
감사합니다.