벽함수(Wall functions)
유동장의 벽면에서의 속도 경계층은 급격하게 변화하며 이를 해결하기 위해서는 벽면에서의 격자를 많이 생성해야 합니다. 이러한 경계층 처리는 계산비용이 상당히 소요되기 때문에 RANS 모델링을 할 때 벽면에서의 전단응력을 처리하는 방법이 있습니다. 대수영역(Log-layer)에 적용할 수 있는 공식을 이용하여 벽면에서의 전단응력을 계산하는 벽함수(wall functions)를 적용하는 방법이 있습니다. 벽함수는 적은 격자를 이용하여 정확한 결과를 얻을 수 있습니다. 예를 들어 벽면에서의 어떠한 유동장을 해석하는데 경계층 격자가 40개 필요로 하면, 벽함수를 적용하면 대략 15개 정도의 격자만 필요합니다. 그러므로 계산비용을 상당히 줄일 수 있습니다. 벽함수를 적용하려면 벽면의 첫 번째 격자는 대수영역(30<y+<300)에 생성하면 됩니다.
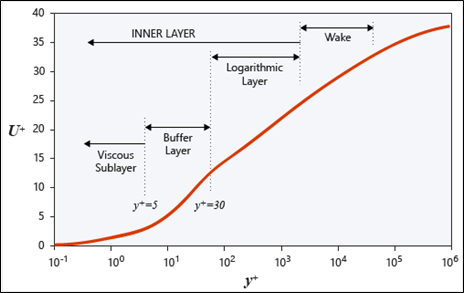
벽 근처의 속도 분포
벽함수는 벽법칙에 따라 유체의 속도(U+)와 벽사이의 거리(y+)의 법칙을 설명하는데 사용합니다. 벽면에서의 유체 유속은 0이며, 벽으로부터 가장 가까운 경계층은 점성저층(Viscous Sublayer: y+<5)입니다. 점성저층은 난류의 영향을 무시할 수 있으며, 유속의 기울기는 선형적인 형태를 나타냅니다. 점성저층과 대수영역 사이를 완충층(Buffer layer: 5<y+<30)이라고 하며, 점성력과 관성력의 중간 사이의 천이 영역입니다. 대수영역(Logarithmic layer: 30<y+<300)은 유체가 난류의 영향을 받고 벽거리에 따라 log 함수로 천천히 변화합니다. 벽함수의 점성영역은 식(1), 대수영역은 식(2)로 정의됩니다.

k는 von Karman 상수(≒0.41)이며 B는 상수로서 매끄러운 벽면에서 5.0을 적용하면 됩니다. 하지만 RANS 난류 모델에서는 난류 모형들의 종속 변수인 k, ε, ω가 벽함수의 관계식에 적용됩니다.
무차원화 벽단위 거리 y+
y+는 벽면에서의 난류의 영향을 평가하기 위하여 벽면에서 영향을 주는 인자들로 구성한 무차원 길이의 개념입니다. 하기의 그림과 같이 y+는 벽면 속도와 벽면으로부터 격자의 거리 그리고 동점성계수로 설명할 수 있습니다. AcuSolve(FEM)에서 y+을 후처리하기 위해서 벽면에서의 노드가 아니라 벽면에서 두번째 노드점에서 계산을 하게 됩니다.
벽함수에 대해서 알아 보았으며 다음 시간에는 수치해석 방법인 FEM, FVM에 대해서 알아보겠습니다.
감사합니다~