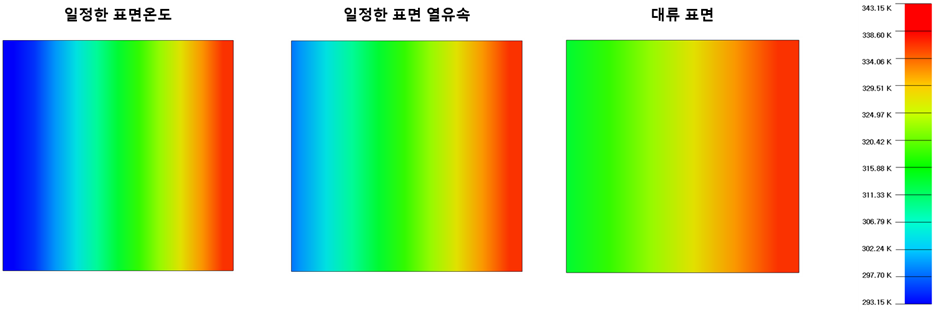경계조건과 초기조건
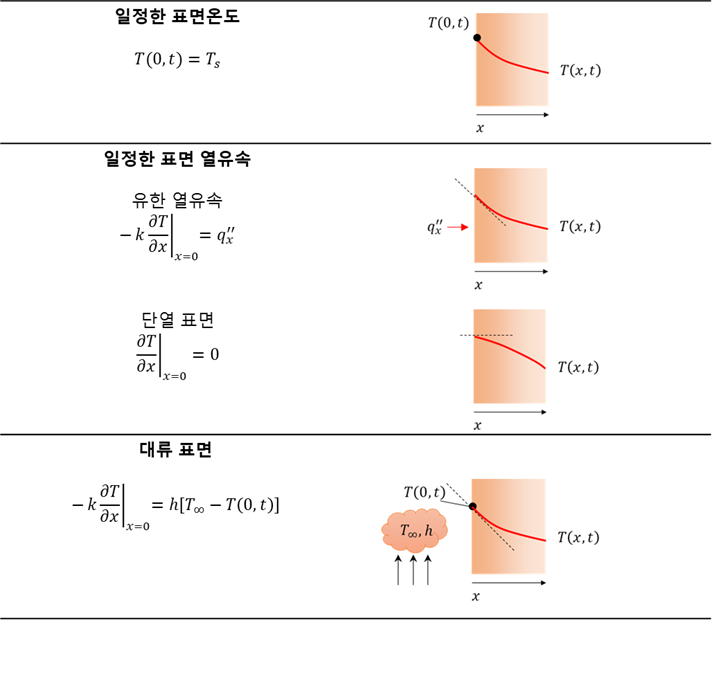
매질 내의 온도분포를 구하기 위해서는 적절한 형태의 열방정식을 풀어야 합니다. 그러나 이러한 풀이는 매질의 경계에 존재하는 물리적인 조건에 의존합니다. 경계조건(boundary condition)은 수학적 형태로 간단하게 표현할 수 있습니다. 열방정식은 공간좌표에 대해서 2계(second order)이기 때문에 계(system)를 기술하기 위해서는 두 개의 경계조건이 필요합니다. 그리고 시간에 대해서는 1계(first order)이기 때문에 초기 조건(initial condition)이 필요합니다. 열전달에서 일반적으로 접하는 세 종류의 경계조건은 다음과 같이 요약하였습니다.
AcuSolve를 이용한 열해석
앞서 설명한 바와 같이 벽면에서 열경계조건은 크게 3가지로 구분할 수 있습니다. 일정한 표면온도, 일정한 표면 열유속 그리고 대류 표면 조건을 CFD 해석 시 벽면 열전달 경계조건으로 사용할 수 있으며 AcuSolve에서도 상기 경계조건을 사용할 수 있습니다.
다음과 같이 직사각형의 2차원 매질이 있습니다. 2차원 매질의 경계조건을 표면온도, 열유속 그리고 대류 표면 경계조건을 적용하여 해석을 수행해 보겠습니다.
Preprocessing
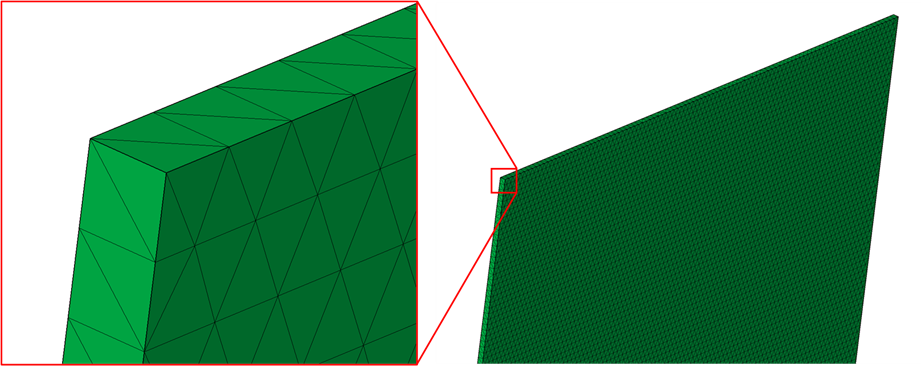
전처리 작업은 SimLab을 활용하였습니다. 2차원 해석을 위해 아래와 같이 x축 0.1 m, y축 0.1 m, 그리고 z축 0.001 m 사각형을 생성하였습니다. 격자는 0.001 m로 사이즈로 설정하여 생성을 하였습니다.
Solving
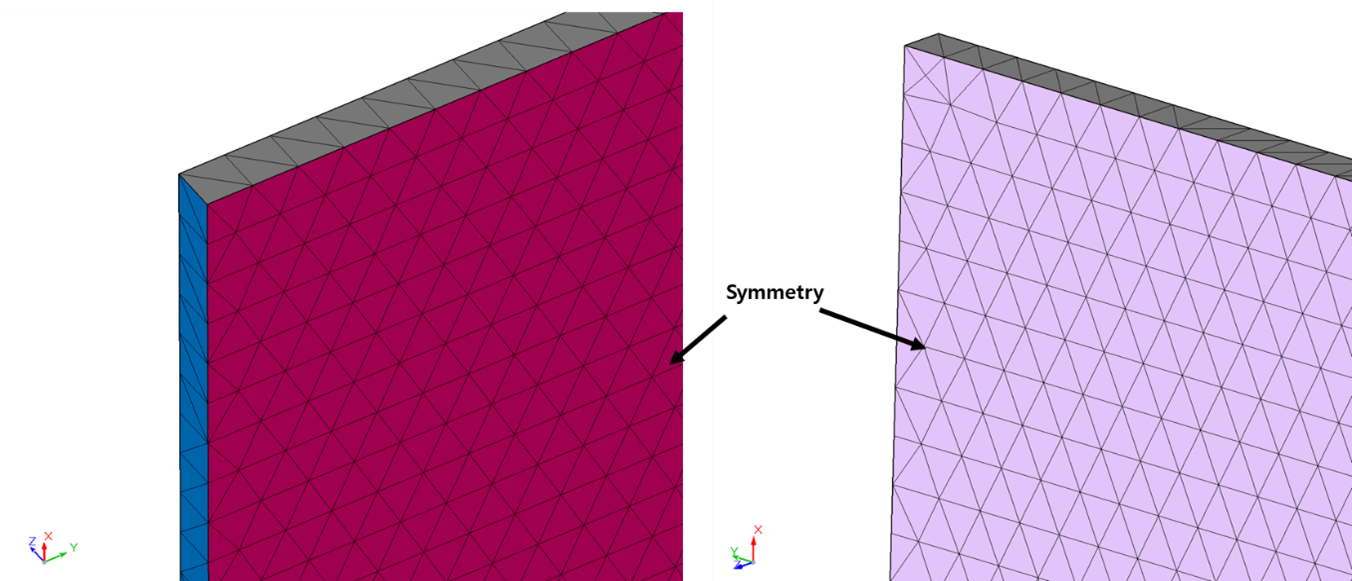
해석은 AcuSolve를 사용했으며, 경계조건은 3가지 조건을 활용하였습니다. (상기 경계조건 참고) 2차원 해석을 위해 z축 방향의 면은 Symmetry 조건을 아래의 그림과 같이 적용하였습니다. 그리고 전도 해석이기 때문에 유동해석은 수행하지 않고 열해석만 수행을 하였습니다.
Postprocessing
아래 그림은 3가지 경계조건에 대한 결과를 나타냅니다. 경계조건을 어떻게 지정하느냐 또는 물리적 수치를 적절하게 주었는지에 따라 온도분포가 달라집니다. 목적에 맞게 경계조건을 설정하면 원하는 결과를 도출하실 수 있습니다.
이번 편을 마지막으로 CFD 블로그는 마무리하도록 하겠습니다. 그 동안 구독해 주셔서 감사합니다.