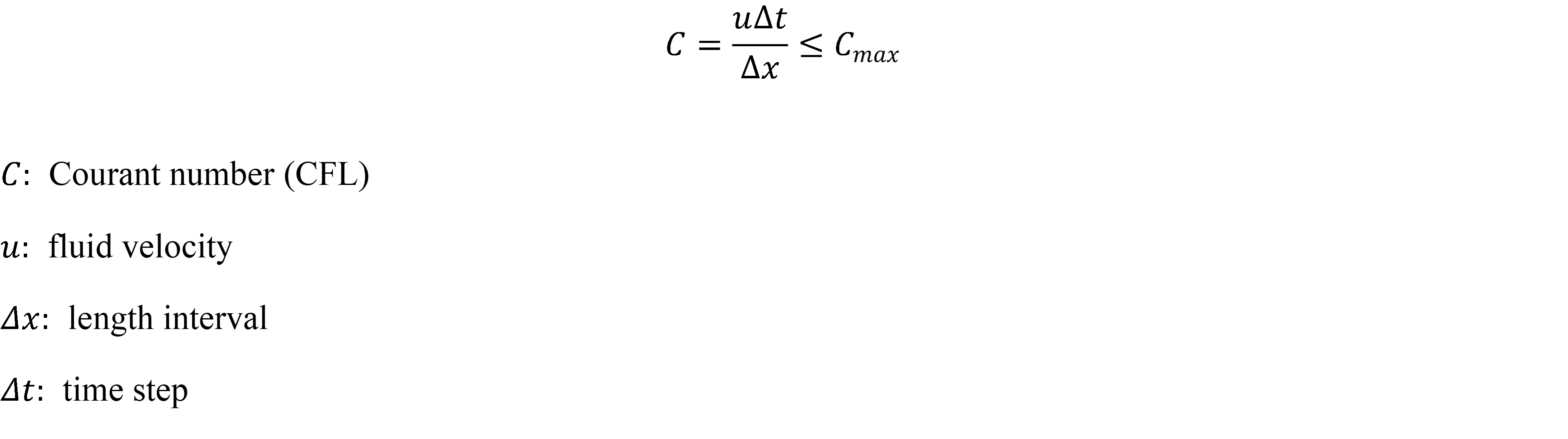양해법 (explicit method)
양해법은 현재 알고 있는 시스템의 상태로부터 미래의 시스템의 상태를 계산하는 방법입니다. CFD 관점에서는 현재의 격자와 주변 격자 정보를 이용하여 미래의 격자정보를 계산합니다. 양해법은 상대적으로 프로그래밍이 쉬운 장점이 있지만 수렴 안정성을 위해 시간 간격(time step)을 작게 사용해야 합니다. 이러한 원인으로 총 해석시간이 오래 걸리는 단점이 있습니다.
음해법 (implicit method)
음해법은 현재 알고 있는 시스템과 미래의 시스템의 상태로부터 미래 시간의 상태를 계산하는 방법입니다. 즉, 현재의 격자 정보와 미래의 주변 격자 정보를 이용하여 미래의 격자 정보를 계산합니다. 음해법은 수렴 안정성이 뛰어나 적절한 시간 간격을 활용하면 총 해석시간이 짧습니다. 양해법을 사용했을 때 발산이 일어나는 격자수에서도 수렴을 시킬 수 있으며, 해석해와의 차이도 합리적인 수준이기 때문에 많이 사용됩니다(AcuSolve). 음해법은 또한 양해법에 비해 큰 시간 간격을 취할 수 있지만, 시간간격이 너무 커졌을 경우 근사 정확도가 나빠질 수 있습니다. 그래서 CFL number를 고려하여 시간간격을 설정해야 합니다.
CFL number (Courant–Friedrichs–Lewy)
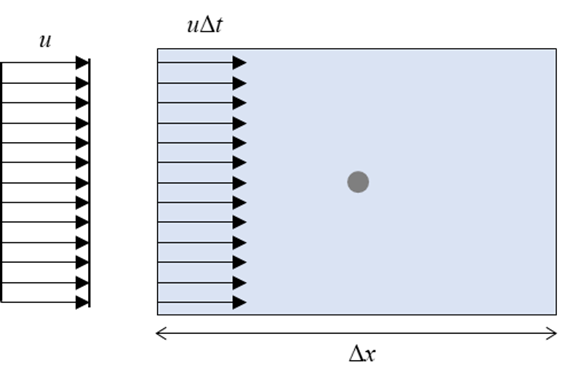
CFL 수는 편미분방정식을 수치적으로 수렴시키기 위한 필요조건으로 계산에 사용되는 시간간격이 특정 시간보다 작아야 한다는 의미입니다. 만약 필요조건을 만족하지 않을 경우 부정확한 해를 구하게 된다는 수치해석학적 조건입니다. CFL 조건은 아래의 식으로 설명될 수 있습니다.
음해법, 양해법 그리고 CFL 수를 알아보았습니다.
다음시간에 봐요~