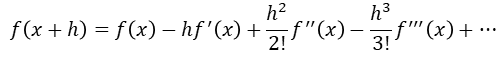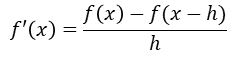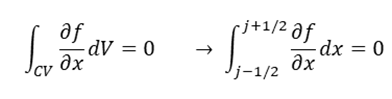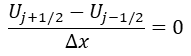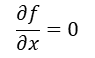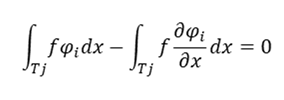유한차분법 (FDM: Finite Difference Method)
미분항을 Taylor 급수전개를 이용하여 표현하는 방법입니다. 즉, 이산화에 요구되는 정확도에 맞추어 격자점이나 그 인접 격자점의 Taylor 급수전개에 의한 관계식을 조합하고 미분항을 근사적으로 표현합니다. 이를 통해 편미분 방정식을 푸는 것을 유한차분법이라고 합니다. 하지만, 해석 대상의 형상이 복잡해질수록 좌표축 방향으로 변화율을 정의하기 어렵고, 격자를 복잡한 형상에 적용하는데 어려움이 있습니다. 또한, 물리량 계산이나 보존법칙을 만족하지 못하는 경우가 발생합니다.
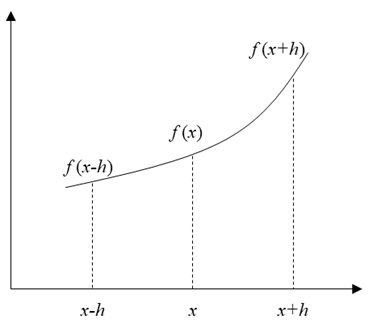
유도과정을 살펴볼 때 f(x)가 존재한다고 가정하고, h만큼 떨어진 거리의 함수가 존재합니다. 거리 x와 x+h을 중심으로하여 talyor급수를 전개하면 아래와 같은 식이 나타납니다.
여기서 h2 이후의 항을 소거하여 식을 정리하면 다음과 같은 식으로 정의됩니다.
따라서 도함수 f’(x)는 전방유한차분법에 의해 근사하여 미분방정식을 풀 수 있습니다.
유한체적법 (FVM: Finite Volume Method)
운동량 및 질량에 대한 보존법칙을 만족시키기 위해 기초방정식을 적분 후 이산화하는 방법을 유한체적법이라고 정의합니다. 격자점을 중심으로 미소영역 내에서 방정식을 적분하고, 그 경계값을 인접 격자점을 이용하여 요구되는 정확도를 만족하도록 적분식을 이산화합니다.
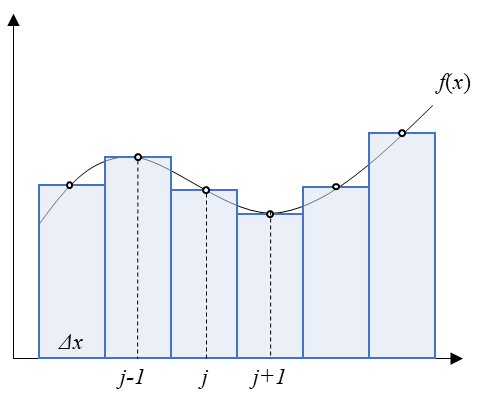
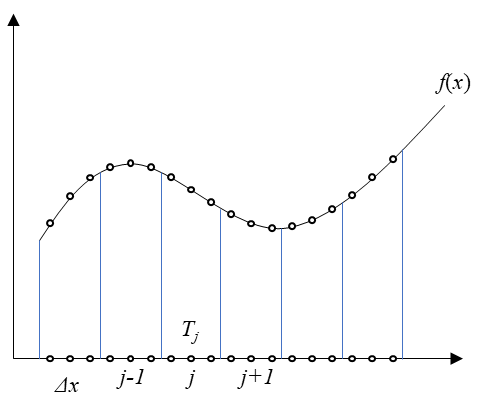
상기 그림과 같이 어떠한 함수의 지배방정식이 있습니다. 이를 계산영역을 구분하여 제어체적을 취할 수 있습니다.
제어 체적을 적분하여 격자점에 대해서 이산화하면 아래와 같이 방정식으로 나타낼 수 있습니다. 이를 모든 격자점의 대수방정식 형태로 나타내어 수치해석을 수행하면 미지수를 구할 수 있습니다.
유한요소법 (FEM: Finite Element Method)
유한요소법은 미지수를 요구되는 정확도의 근사함수로 표현하고, 그 계수의 크기를 가중잔차법(weighted residual method) 등을 이용하여 미소영역마다 결정하는 것입니다. 대부분의 경우 삼각형의 미소영역을 조합하여 계산영역을 구성하며, 유동장이 복잡한 형상에서도 최적으로 대응할 수 있는 특징을 갖고 있습니다. 전통적인 유한요소법은 주어진 편미분 방정식에 임의의 테스트 함수를 곱한뒤, 이를 계산공간에서 적분하여 weak variational formulation으로 불리는 형태로 바꾸어 그 근사해를 찾습니다. 이는 통상적으로 Galerkin 유한요소법이라고 불리며, AcuSolve는 이 방법을 이용하고 있습니다.
상기 함수와 같이 요소 내부로 구분하여 테스트함수를 통해 적분형 지배 방정식을 유도합니다. 각 요소를 이산화하여 수치해석을 수행하여 미지수를 구할 수 있습니다.
감사합니다~