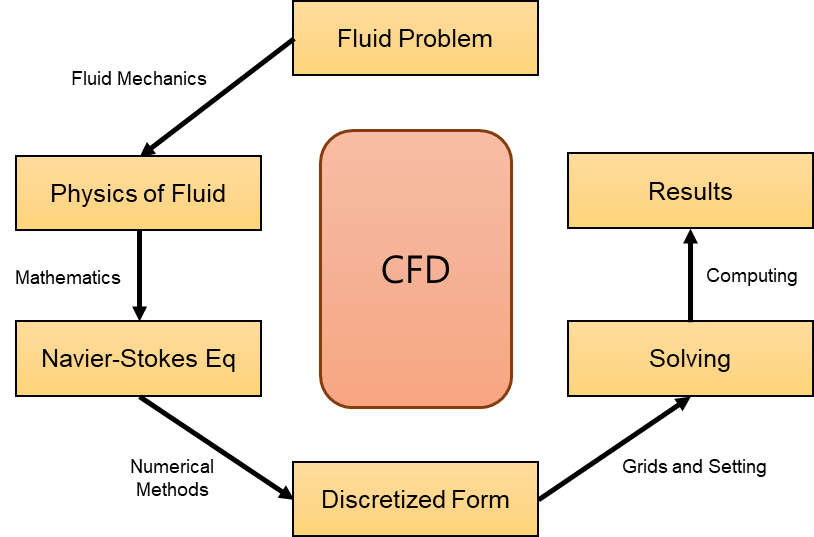
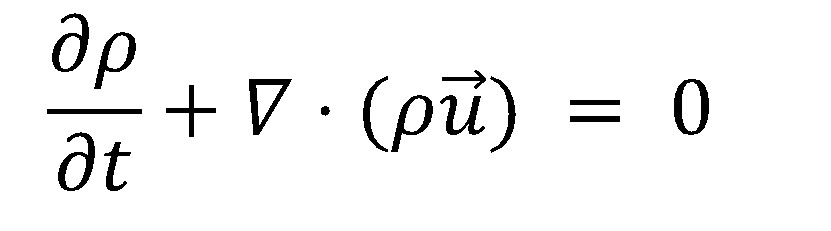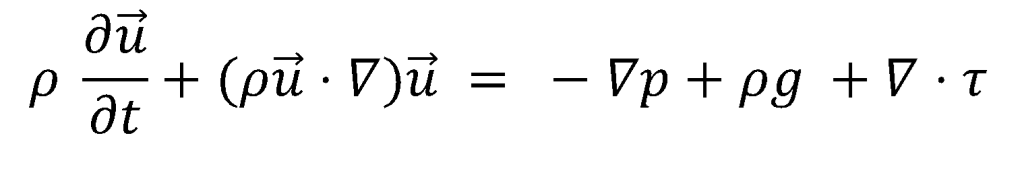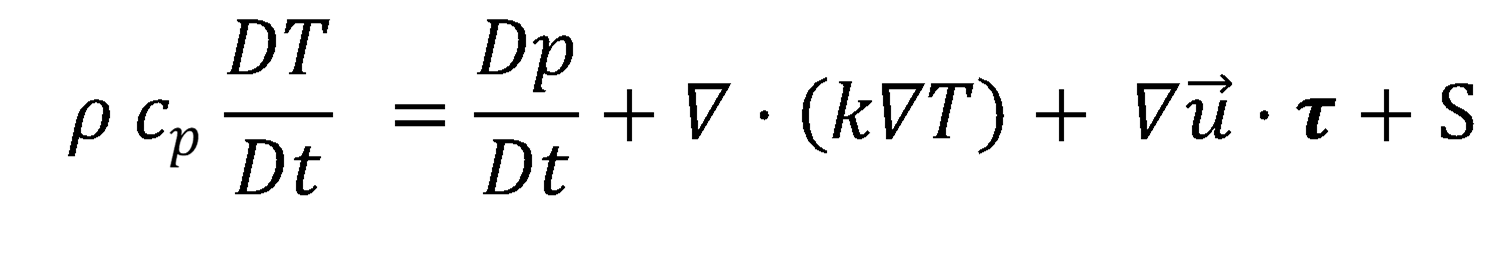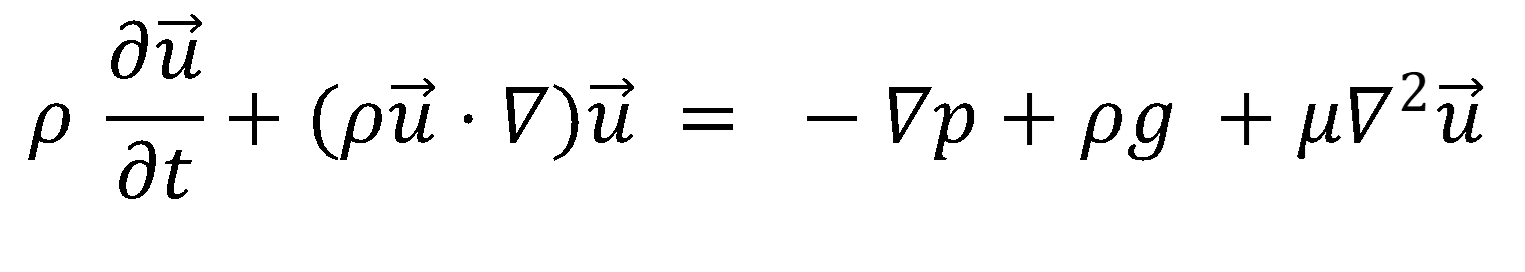CFD 측면에서 유체 문제를 해결하기 위해서는 나비에-스토크스 방정식을 이해할 필요가 있습니다. 나비에-스토크스 방정식을 이산화하여 대수방정식으로 변환하고 수치기법을 통하여 유동 문제를 해결합니다.
일반적으로 유체의 지배방정식은 연속 방정식, 운동량 방정식, 에너지 방정식 세가지로 구성되어 있습니다. 이를 점성을 가진 유체의 운동을 기술하는 편미분 방정식인 나비에-스토크스 방정식으로 나타낼 수 있습니다. 유체역학의 기본인 지배방정식을 간단하게 살펴보고 나비에-스토크스 방정식을 알아보도록 하겠습니다.
1) 연속 방정식(Continuity Equation)
연속 방정식은 유체의 물리량이 보존되는 상태로 이송되는 것을 기술한 형태입니다. 밀도가 일정할 때 어느 구역에서 유체의 유량은 일정하다는 의미입니다. 그래서 질량 보존을 표현하는 방정식이 연속 방정식으로 불립니다.
2) 운동량 방정식 (Momentum Equation)
운동량 방정식은 뉴턴의 운동 2법칙을 유체의 물리량에 맞게 표현하면 위의 식으로 나타낼 수 있습니다. 유체 시스템이 받는 힘을 두가지로 나눌 수 있는데, 시스템 부피 전체가 받는 체적력(body force)과 표면력(surface force)으로 구분할 수 있습니다. 체적력은 시스템의 질량에 비례하고, 간접적으로 작용하는 힘인데 대표적으로 중력, 원심력, 전향력 그리고 전자기력 등이 있습니다. 표면력은 시스템의 표면적에 비례하고, 직접적으로 면에 작용하는 힘인데 대표적으로 압력, 표면장력, 수직응력 그리고 전단응력 등이 있습니다.
3) 에너지 방정식 (Energy Equation)
에너지 방정식은 열역학 1법칙에서 유체의 물리량에 맞게 표현하면 위의 식으로 나타낼 수 있습니다. 유체 시스템의 열전달률과 일률 그리고 운동에너지와 내부에너지의 관계로 에너지 방정식을 표현할 수 있습니다. 열전달률은 푸리에 열전도 법칙을 이용하며, 일률은 유체의 운동량 보존으로부터 유추할 수 있습니다.
4) 나비에-스토크스 방정식 (Navier-stokes Equation)
응력텐서(τ)와 유체의 거동 사이의 관계를 운동량 보존 방정식에 적용하면 나비에-스토크스 방정식이 됩니다. 유체의 응력텐서는 크게 압력과 점성으로 나타낼 수 있습니다. 비압축성 뉴턴 유체에 대한 응력텐서를 운동량 방정식에 대입하고 정리하면 위에 기술된 식으로 표현이 가능합니다. 나비에-스토크스 방정식은 비선형 편미분 방정식의 형태이며, 뉴튼의 제2법칙으로 설명이 가능합니다. 하지만 복잡한 식과 미지의 변수들로 인하여 사람의 손으로 계산하기 너무 어렵습니다. 그래서 컴퓨터의 수치적인 계산을 통하여 유체 문제를 해결할 수 있습니다.
감사합니다.
한국알테어